[1]    D.BAILEY, J.BORWEIN, P.BORWEIN and S.PLOUFFE, The Quest for 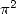, in The Mathématical Intelligencer, vol.18,n 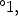1997

[2]    D.BAILEY, P.BORWEIN, and S.PLOUFFE, On The Rapid Computation of Various Polylogarithmic Constants, 1996
http ://www.cecm.sfu.ca/personal/pborwein/

[3]    D.J.BROADHURST, Polylogarithmic ladders, hypergeometric series and the ten millionth digits of 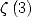and 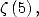preprint, March 1998.
http ://front.math.ucdavis.edu/math.CA/9803067

[4]    L.LEWIN, Structural Properties of Polylogarithms, 1991 AMS

[5]    B.GOUREVITCH, Une formule BBP pour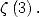
../../perso/zeta.ps

[6]    V.ADAMCHIK, 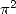 : A 2000-Year Search Changes Direction, in Education and Research, vol. 5, n.1, 1996

[7]    G. ALMKVIST, C. KRATTENTHALER, J. PETERSSON, ”Some new formulas for 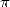”, preprint, Matematiska Institutionen, Lunds Universitet, Sweden. and Institut fur Mathematik der Universitat Wien, Austria.

[8]    J.BORWEIN, D.J.BROADHURST, J. KAMNITZER, ”Central Binomial Sums, Multiple Clausen Values and Zeta Values”, Avril 2000

[9]    I.S. GRADSHTEYN, I.M. RYZHIK, ”Table of integrals, Series and Products”, Alan Jeffrey Editor, 5e ed, 1994

[10]   O. ESPINOSA, V.H. MOLL, ”On some integrals involving the Hurwitz Zêta Function”, Part 1, Ramanujan Journal, 2001.

[11]   D.H. BAILEY, R.E. CRANDALL, ”On the random character of fundamental constant expansions”, Experimental Mathematics 10 :2, page 175.
http ://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf

[12]   G. HUVENT, Formules BBP, Seminar ANO, IRMAR, Lille University.
http ://ano.univ-lille1.fr/seminaries/expo_huvent01.pdf

[13]   B. GOUREVITCH, J. GUILLERA, ”An extend of BBP sums to binomial sums”, preprint.

[14]   R. APERY ”Irrationalité de 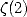et 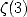” Astérisque 61, 11-13, 1979.

[15]   K.S. KOLBIG ”The polygamma function and the derivatives of the cotangent function for rational arguments” CERN-IT-Reports, 1996.