Joseph Fourier
(1768 - 1830)

ce qui s'écrit en complexe et pour une fonction de période T :

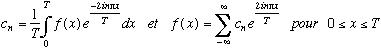
Tranches de vie

Fourier occupe une place à part dans le monde mathématique et aussi dans celui des suites convergeant vers .
Né en 1768, Fourier était obsédé par l'étude de la chaleur. Alors que son logement à Grenoble était surchauffé au point d'incommoder ses visiteurs, il s'engonçait dans de lourds vêtements. Cependant, pour étudier ces phénomènes, il mit au point une méthode de décomposition d'un signal périodique en somme de signaux plus élémentaires, notamment de type sinusoïdal.
Le technicien a rarement besoin de plus de quelques signaux pour reconstituer le signal voulu avec une approximation satisfaisante. Le mathématicien dispose, lui, de la décomposition exacte en signaux de plus en plus faibles. Si l'on a une fonction f continue, périodique de période 2 et dérivable, elle peut se décomposer comme ci-dessus. La formule reste valable si f est continue et dérivable par morceaux, on remplacera simplement dans le cas où x est un point de discontinuité f(x) par (f(x-)+f(x+))/2.
Remarquons que cette théorie audacieuse a reçu un accueil plus que mitigé à son époque. Nombre de mathématiciens parisiens célèbres, parmi lesquels Lagrange, Laplace, Legendre, Biot et Poisson, n'acceptaient pas cette conjecture, et lorsque Fourier l'exposa devant l'académie des Sciences, Lagrange se leva et déclara qu'il la tenait pour fausse!
A cause du chauffage excessif, Fourier mourut d'un arrêt du coeur en 1830 !

Autour de

Aujourd'hui, si l'on veut retrouver les innombrables formules contenues dans les ouvrages d'Euler, par exemple, on utilise la théorie de Fourier. La formule générale permet en effet par de nombreux cas particuliers de calculer les limites de presque toutes les séries...
De plus, il est amusant de constater qu'encore aujourd'hui, les techniques d'accélération des calculs dans les algorithmes actuels reposent sur les transformées de Fourier rapides (TFR), et permettent d'atteindre les milliards de décimales calculées sur les ordinateurs... décidément très utile ce monsieur Fourier !

Démonstration

Nous ne nous arrêterons pas sur la démonstration de la formule, appelée "Théorème de Dirichlet", assez longue et pas en rapport direct avec . Néanmoins, détaillons un tout petit peu :

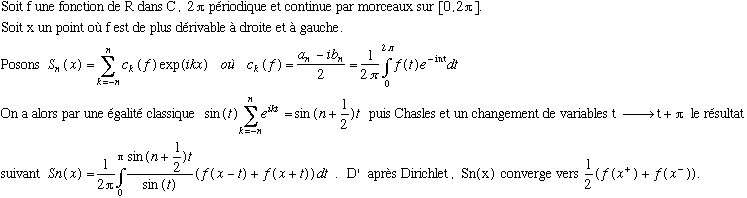
Applications

C'est ici qu'intervient pour nous tout l'intérêt de la théorie de Fourier ! Il suffit en effet maintenant de choisir une fonction vérifiant les conditions du théorème et de calculer ses coefficients de Fourier. Puis on choisit un x particulier :





3) Formule de Leibniz

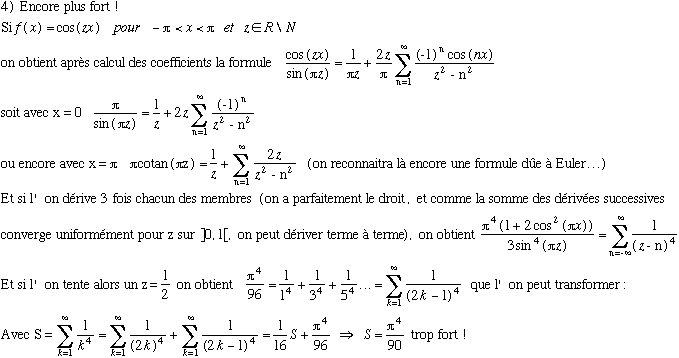
Essais

se reporter à Euler pour les essais de rapidité de convergence des séries engendrées par les formules de Fourier...