Jacques Bernoulli
(1654 - 1705)

Les polynômes de Bernoulli B_n sont définis par récurrence d'après :

Les nombres (Ber_n) sont alors définis par Ber_n=B_n(0)
Autre définition équivalente :
Les nombres de Bernoulli Ber_k sont définis comme des coefficients dans la série entière
=
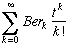
Pour plus d'infos sur les numérateurs et dénominateurs des nombres de Bernoulli, cf. A027641 et A027642 ou encore pour les Ber_2n A000367 et A002445.

Tranches de vie

Premier de la lignée des célèbres mathématiciens suisses du même nom, Jacques (Jakob) est originaire d'Anvers mais s'exile sous la dictature du duc d'Albe en Flandre. Abandonnant la théologie chère à son père, il se tourne vers les mathématiques et la physique. Il tirera de son intérêt pour l'astronomie sa devise "Invito patre sidera verso" (j'étudie les étoiles contre la volonté de mon père). Devenu professeur à l'université de Bâle, il s'intéresse au calcul infinitésimal qu 'il met en rapport avec les courbes (Lemniscate...) et qui lui permet d'introduire les coordonnées polaires. Il étudie également les probabilités et les séries numériques, ce qui le pousse à définir les fameux nombres de Bernoulli décrits plus haut.
* Photos de Johann (1667-1748) et Daniel (1700-1782) Bernoulli

Autour de

Plusieurs formules d'analyse font apparaître ces nombres de Bernoulli, notamment dans de nombreuses limites de séries comme l'a montré Euler. Son apport à la recherche sur est donc fondamental même s'il reste indirect. On lui doit la démonstration de la convergence de dont la limite et celles des suites de ce type seront trouvées par Euler.
Les premiers nombres de Bernoulli sont :

B₀=1
B₁=-1/2
B₂=1/6
B₄=-1/30
B₆=1/42
B₈=-1/30
B₁₀=5/66