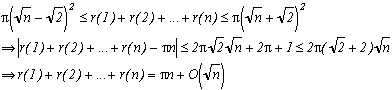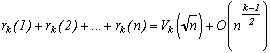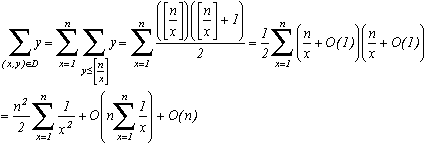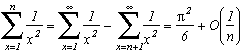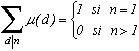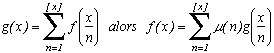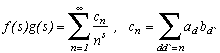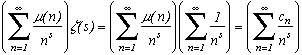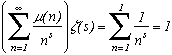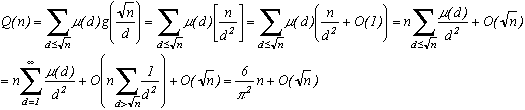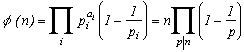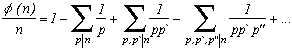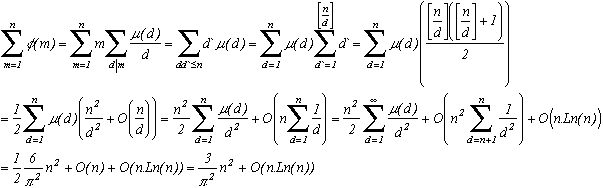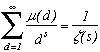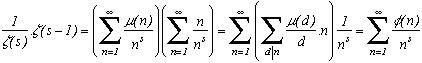Gauss (1777 - 1855) Möbius (1790 -1868) Euler (1707 - 1783)

Fonctions arithmétiques et Pi
r(n) de Gauss / Somme des diviseurs / Möbius / Indicatrice d'Euler

1) Fonction r(n) de Gauss

Soit r(n) le nombre de décompositions d'un entier n sous forme de 2 carrés,
alors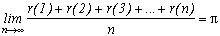

2) Fonction (n) somme des diviseurs

Soit (n)= c'est à dire la somme des entiers positifs qui divisent n.
Alors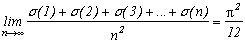

Pour plus d'infos sur la fonction (n) de Möbius, cf.A000203

3) Fonction µ(n) de Möbius

Soit µ(1)=1 ; µ(n)=0 si n possède au moins un facteur carré >1
et µ(p₁p₂...p_k)=(-1)^k si p₁, p₂, ..., p_k sont des nombres premiers distincts.
(exemple µ(2)=µ(7)=-1, µ(4)=µ(8)=0, µ(6)=µ(10)=1)
Alors pour s>1 par exemple.
Beaucoup de résultats très impressionnants concernant cette fonction existent. Parmi eux, on peut citer aussi l'étonnante formule qui suit : en considérant Q l'ensemble des entiers nN* qui n'ont pas de facteur carré dans leur décomposition (c'est à dire tels que µ(n)=1) on obtient la jolie formule suivante :

Cette approche permet aussi d'établir le magnifique théorème : La probabilité pour qu'un entier soit sans facteur carré est

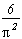
Pour plus d'infos sur la fonction de Möbius, cf.A008683

4) Fonction (n) indicatrice d'Euler

Soit (n) le nombre d'entiers strictement inférieurs à n et qui sont premiers avec n (n'ont pas de diviseur commun avec n). Pour plus d'informations sur la fonction d'Euler cf.A000010
Alors soit par exemple et
Cette fonction permet là encore de redémontrer aussi habilement le théorème de Cesàro.

Quelques mots sur Möbius

Ce cher Möbius est un mathématicien Allemand né en 1790 en Saxe. Il fit ses études à Göttingen sous la direction de Gauss et devint astronome à Leipzig. Vivant de cette science, c'est néanmoins un passionné de mathématiques qui s'intéresse à la géométrie projective et à la théorie des nombres en introduisant sa célèbre fonction.

Autour de

Les fonctions arithmétiques étudiées aux XVIIIe et XIXe siècle ont souvent une définition assez simple mais leurs propriétés semblent toujours sorties un peu de nulle part. Comment imaginer en effet que des propriétés sur les entiers puissent rejoindre le monde des réels ? Bien évidemment, il ne faut pas compter sur elles pour battre des records de calcul de décimales, mais chose étonnante, certaines qui sont présentées ici parmi les plus célèbres, ont un rapport étroit avec Pi !
C'est la plupart du temps dû aux valeurs de la fonction Zêta de Riemann, mais pour en arriver là, examinons plus en détail chaque fonction :

Démonstrations

1) Fonction r(n) de Gauss

Donc, on rappelle que r(n) est le nombre de décompositions d'un entier n sous forme de 2 carrés, combinaisons comprises. C'est à dire que l'on inclut dans ce nombre les combinaisons triviales avec les multiplications par -1 ou les ordres des carrés.
Par exemple, pour 5, on a :
5=(+/-1)²+(+/-2)²=(+/-2)²+(+/-1)²
donc r(5)=4+4=8.
Les propriétés de la fonction ont été étudiées par Gauss et Jacobi notamment.
Le premier a démontré le résultat qui nous intéresse, et qui a une explication géométrique agréable.

Si l'on considère un disque de rayon , c'est à dire d'équation x²+y²=, on voit que les couples (x,y) d'entiers qui vérifient x²+y²= où pn sont dans le disque d'après la figure ci-contre (ils sont sur le bord du cercle de rayon qui est plus petit que celui de rayon , ce sont les point à l'intérieur du cercle). Dessinons pour chacun de ces points dans le disque un carré dont le coin inférieur gauche est ce point.
On obtient alors une drôle de figure, que l'on appellera domaine D_n, dont l'aire est le nombre de carrés (de côté et donc d'aire 1) qu'il contient.
Mais r(p) pour pn compte le nombre de points qui sont sur le cercle de rayon donc tout point à l'intérieur du disque est comptabilisé dans un r(p) pour pn. Donc, le nombre de points et de carrés associés est r(1)+r(2)+...+r(n).
L'aire du domaine D_n représenté plus haut est donc r(1)+r(2)+...+r(n).
Mais D_n est compris dans un cercle de rayon , c'est à dire le rayon du premier cercle + la diagonale d'un carré de côté 1 (Regardez la figure, la seule chose du domaine qui déborde du cercle ne dépasse jamais de plus d'une diagonale d'un carré, comme marqué)
De même, ce domaine peut contenir le cercle de rayon . Ces disques ont pour aire donc finalement, on a comme encadrement de l'aire de D_n :

Et voilà !
On a bien
Au lieu de considérer O(), on pourrait chercher pour quelle puissance de n minimale (notons-la a) le résultat est encore valable, en d'autres termes, quelle est la vitesse de convergence.
Comme le rappelle Autour du nombre Pi de Eymard/Lafon, c'est l'objet de nombreuses recherches depuis un siècle et demi.
On vient de montrer que a1/2. Hardy et Landeau ont prouvé indépendamment de leur côté que a1/4. On conjecture fortement que a=1/4 mais cela n'a pas encore été démontré. Le meilleur coefficient connu est actuellement a22/73 et provient de Huxley (1993).

Dans le même ordre, on peut généraliser à r_k(n) le nombre de décomposition de n par la somme de k carrés. Cela revient à travailler non plus dans R² pour deux carrés, mais dans R^k.
On obtient de même
avec V_k(R) le volume d'une boule de rayon R en dimension k.
Mais d'après le grenier, on sait que cela vaut :

pour la dimension m.
Donc, on en conclut ici :

avec

---

2) Fonction (n) somme des diviseurs

On rappelle encore une fois que (n)=, c'est à dire la somme des entiers positifs qui divisent n.
Quelques exemples, pour y voir un peu plus clair !
(1)=1, (2)=1+2=3, (6)=1+2+3+6=12, (12)=1+2+3+4+6+12=28
Cette fonction est multiplicative pour deux entiers premiers entre eux.

Entrons dans le vif du sujet et faisons un peu de dénombrement
(1)+(2)+...+(n) contient les diviseurs de chaque entiern comptés un certain nombre de fois, et on en fait la somme. on va chercher à déterminer ce "certain nombre de fois" par diviseur.
Fixons ainsi un x entre 1 et n, on cherche d'abord les y_p tels que xy_p=p, pn.
Donc pour l'ensemble des pn, on aura bien compté toutes les fois qu'apparaîssent les diviseurs y_p des (p) en même temps que le diviseur x. Ensuite, on somme les y_p sur tous les x, et on obtient la valeur voulue de (1)+(2)+...+(n).

Considérons donc la droite xy=n dans le plan comme ci-contre.

Fixer x revient à compter les y tels que xyD.



Ainsi en notant [a] la partie entière de a, on a
(1)+(2)+...+(n)=

mais on sait que par majoration terme à terme donc

On sait également que gamma, la constante d'Euler, vaut
donc et finalement

(1)+(2)+...+(n)=n²+O(n.Ln(n))

chouette, encore une autre de faite...
Comme pour le 1), d'intenses recherches s'effectuent autour du meilleur reste possible et pour l'istant, A. Walfisz détient la palme avec O(n.Ln^2/3(n)) trouvé en 1963.

---

3) Fonction µ(n) de Möbius

Soit µ(1)=1 ; µ(n)=0 si n possède au moins un facteur carré >1 et µ(p₁p₂...p_k)=(-1)^k si p₁, p₂, ..., p_k sont des nombres premiers distincts (exemple µ(2)=µ(7)=-1, µ(4)=µ(8)=0, µ(6)=µ(10)=1).
Lemmes
1) Une des premières propriétés (très chouette) de cette fonction est la suivante :

La démonstration est simple, le résultat est évident par définition pour n=1. Prenons maintenant un n>1 et montrons que la somme est nulle.
L'entier n se décompose comme d'habitude en un produit de fateurs premiers donc on peut l'écrire :
n=p₁^a1p₂^a2...p_k^ak. Si l'on veut écrire la somme sur les diviseurs de n, cela correspond à prendre la somme sur les premiers p_i, puis sur les couples de premiers p_ip_j , les triplets, etc.. soit :

d'après la définition µ(p₁p₂...p_k)=(-1)^k et ensuite on compte le nombre de couples, triplets qu'il peut exister dans la somme (d'où les combinaisons) et enfin, on reconnait la formule du binôme de Newton.

2) µ est une fonction multiplicative, et fournit un résultat assez fort qui pemet d'inverser certaines formules :

(effectivement, on a )
Démo :
Bon, c'est une bonne chose, passons maintenant aux démos qui nous intéressent :

Preuve de :

On aura besoin d'un petit lemme, que l'on pourrait appeler lemme de Dirichlet :
Soit f(s) et g(s) les séries dites de Dirichlet définies par :
. La multiplication de ces deux séries donne :

Calculons maintenant en utilisant cette multiplication de Dirichlet :

avec donc finalement

d'où le résultat

---

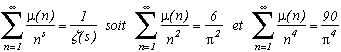
Allons encore plus loin, comme je l'ai dit plus haut, en considérant Q l'ensemble des entiers nN* qui n'ont pas de facteur carré dans leur décomposition (c'est à dire tels que µ(n)=1) on obtient la jolie formule suivante :

La démonstration n'est pas très difficile mais elle oblige à une généralisation longue de certains résultats, et pour l'instant, je n'ai pas envie que cette page devienne un monstre...Je ne résisterai pas par contre au plaisir de pouvoir donner un petit résultat que je trouve encore plus impressionnant :

La probabilité pour qu'un entier soit sans facteur carré est

Démo :

On définit Q(x) pour x réel comme le nombre des entiers k inférieurs à x et qui sont sans facteurs carrés. D'après la définition même de la fonction de Möbius, on peut écrire pour n entier :
Q(n)=. Pour montrer le théorème, il suffit de regarder la proportion de Q(n) par rapport à n, c'est à dire montrer que

Q(n)=n+O(n^1/2)

Le principe consiste tout d'abord à ranger un entier k dont le plus grand facteur carré est d² dans un ensemble E_d. On fait cela pour tout kn. Pour E₁, bien sûr, cela correspond à l'ensemble des entiers sans facteurs carrés. Et puisqu'il n'y a pas de facteur carré supérieur à n^1/2 dans n (forcément !), E_d est vide pour d>n^1/2. Comptons le nombre d'éléments de Ed :
Il est tout d'abord clair que card(E₁)=Q(n).
Pour les autres E_d, prenons k=d²*k' dans E_d.
k'n/d² car kn.
D'autre part, k' n'a pas de facteur carré car si il en avait un (notons le a par exemple), a.d serait aussi un facteur carré de k et puisque a.d>d, k appartiendrait à un autre E_i. Donc finalement card(E_d)=nombre de k'n/d² sans facteur carré, donc : card(E_d)=Q(n/d²)

Comme on a n entiers non nuls inférieurs à n (!), et qu'ils sont tous compris dans un E_d, on peut écrire :

Ensuite, on applique la fameuse formule d'inversion de Möbius à f(x)=Q(x²) avec n^1/2=x
et donc à g(n)=n², g(x)=[x²] pour x réel.

Cette formule permet le calcul suivant, dont les intermédiaires sont (il me semble...) assez évidents :


Enfin, pour le O(somme), le résultat provient tout de même de :

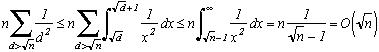
4) Fonction (n) indicatrice d'Euler

Rappel : (n) le nombre d'entiers strictement inférieurs à n et qui sont premiers avec n (n'ont pas de diviseur commun avec n).

Lemmes :
1) Un premier lemme énonce que est multiplicative pour deux entiers m et n premiers entre eux, c'est à dire

(n.m)=(n).(m)

En effet, si l'on cherche à évaluer (n), on part de la définition : d'après le théorème de Bézout, k et n sont premiers entre eux si et seulement si il existe u et v entiers tels que u.k+v.n=1 donc c'est équivalent à k inversible modulo n.
Donc (n) est le cardinal du groupe des inversibles de Z/nZ. Comme m et n sont premiers entre eux, d'après le fameux lemme chinois, il existe un isomorphisme entre Z/mnZ et Z/nZ*Z/mZ donc les groupes inversibles de ces deux anneaux ont même cardinal et (n.m)=(n).(m).
(ouf, voilà quelques souvenirs douloureux d'algèbre !)

2) Maintenant, si l'on veut évaluer pour tout n, commençons par décomposer ce pauvre entier : n=p₁^a1p₂^a2...p_k^ak , a_i entier non nul, et calculons pour p_i^ai :
Entre 1 et p_i^ai (non compris), il y a p_i^ai-1 entiers (!) et comme seuls les multiples de p_i sont diviseurs de p_i^ai car p_i premier, ces diviseurs sont :
pi, 2pi, 3pi, ..., (p_i^ai-1)p. Il y en a donc p_i^ai-1.
Donc le nombre d'entiers premiers avec n est :

(p_i^ai)=p_i^ai-1-nombre de diviseurs de n=p_i^ai-1-(p_i^ai-1-1)=p_i^ai(1-1/p)

Et comme les p_i^ai sont forcément premiers entre eux, on peut calculer (n) grâce à la multiplicité de :

Par exemple, 500=2²5³ donc (500)=500(1-1/2)(1-1/5)=200.

3) Développons le produit ci-dessus, on obtient :

Si l'on a d=p₁p₂...p_k, les p_i étant tous distincts comme dans la somme, alors µ(d)=(-1)^k donc .
Donc, dans tous les cas, on peut écrire :

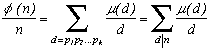
car si d a un facteur premier carré, la fonction de Möbius appliquée à d est nulle d'après la définition.
Cool...

Démo :
Bon, alors il s'agit maintenant de montrer puis ...

On commenca à s'en douter depuis le temps, le lemme précéent faisant intervenir la fonction de Möbius va sacrément intervenir !
Lançons-nous hardiment dans les calculs :


Ouf...
Là encore, de nombreuses recherches ont abouti à un nouveau coup d'éclat de Walfisz (1963) qui trouva le meilleur reste connu actuellement , O(n(Ln(n))^2/3(Ln(Ln(n)))^4/3).

Pour prouver la seconde formule, on va utiliser la multiplication de Dirichlet et le résultat que l'on a montré un peu plus haut :

et voilà ! Pas trop difficile, n'est-ce-pas ? Mais il faut simplement réellement s'y plonger...

Cette dernière formule permet par exemple de trouver :

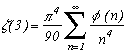
Une dernière conséquence de ce résultat, le fameux théorème de Cesàro ! Incroyable de le retrouver ici, mais la définition de la fonction indicatrice d'Euler le laissait présager. En effet, comptons le nombre de couples d'entiers (p,q) compris entre 1 et n. Si p=1, q peut prendre les valeurs 1 à n, soit n valeurs. Si p=2, q peut prendre les valeurs 2 à n (car (2,1) a déjà été compté sous la forme (1,2) précédemment lorsque p=1) soit n-1 valeurs, et ceci jusqu'à p=n. Donc il y a 1+2+3+...+n=n(n+1)/2 couples (p,q).
Le nombre d'entiers premiers avec p fixé est tout simplement la valeur de la fonction (p) par définition. Donc jusqu'à n, le nombre de couples d'entiers (p,q) premiers entre eux est (1)+(2)+(3)+...+(n).
Donc la probabilité pour que deux entiers positifs soient premiers entre eux vaut la limite de la proportion de la somme des (k) (cas favorables) sur le nombre n(n+1)/2 de couples (p,q) (cas totaux) soit :

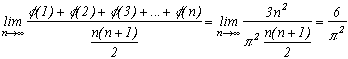
Chouette...

Essais

Pouf, même pas la peine ! Les fonctions arithmétiques ne sont pas du tout faites pour cela et dépendent d'ailleurs pour la plupart d'entre elles de la série (s) donc connaissent également une convergence logarithmique navrante...