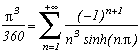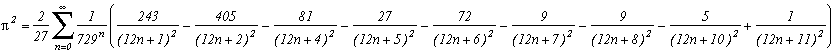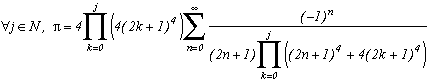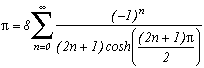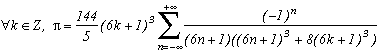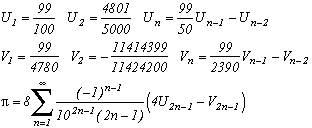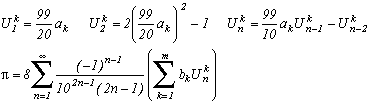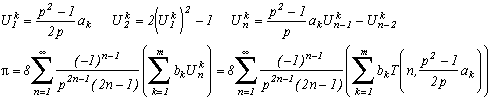Formulas giving Pi
based on analytical methods
(By chronological order of authors or people who inspired them)

Other continued fractions

Newton : (1642 - 1727)

   

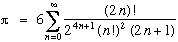
suite similaire :

Leibniz (1646 - 1716)

Katahiro (1664 - 1739)

Machin (1680 - 1751)

Moivre/Stirling (1667 - 1754) / (1692 - 1770)

Euler (1707 - 1783)

1) 1739
and more generally, we have
where Ber_2i is the Bernoulli's number with index 2i

(see appendix: Numbers of Bernoulli)

2)


3) et 4) (1737)

Buffon (1707 - 1788)

If a needle of length 2a is dropped on a parquet formed of floorboard of width 2b, the probability that the needle cuts one of the lines of this parquet is

Gauss (1777 - 1855)

Cesaro (1859 - 1906)

The probability that two integers ramdomly chosen are prime between them is ...

Ramanujan (1887 - 1920)

   



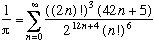
Writing (x)_n the value :
we can write:

Gosper

We have a general formula for x less than 1:

where ₂F₁ is a hypergeometric seie, which distract us from our topic, so I won't mention it....
For x=1/2, we get :
which has a convergence of 2n
For we can write :
of convergence 3.39n

William Gosper is also used to formulae that are a bit wierd making use of , donc ask me of their use!
For example :






and by generalising :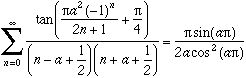

Sums of Reynolds :

G and D. Chudnovsky

Borwein

with A=63365028312971999585426220+28337702140800842046825600*5^1/2 + 384*5^1/2(10891728551171178200467436212395209160385656017 + 4870929086578810225077338534541688721351255040*5^1/2)^1/2
B=7849910453496627210289749000+3510586678260932028965606400 + 2515968*3110^1/2(6260208323789001636993322654444020882161 + 2799650273060444296577206890718825190235*5^1/2)^1/2
C=-214772995063512240-96049403338648032*5^1/2-1296*5^1/2(10985234579463550323713318473 + 4912746253692362754607395912*5^1/2)^1/2

Plouffe

Brown

So, lets take a natural integer n different from 0. For example 10. So far everything is all right !

Now let's considerthe nearest "multiple" bigger than or equal to n-1.

In our case, we find 18 because it is a "multiple" of 9=10-1 and bigger than 10.
Let us repeat this considering the nearest "multiple" bigger or equal to n-2, here 24, then of n-3 (28), of n-4 (30) and so on for n-k unto we get to k=n-1. We call f(n) the result (f(10)=34)
Well, funnily enough,

Woon

Bellard

with

Mandelbrot/Bolle

let us consider the point c=(-0.75,X) of the complex plane, that is a point straight over the "neck" of the Mandelbrot set.
Let n be the number of iterations from which the characteristic quadratic sequence of the Mandelbrot set Zn+1=Zn2+c with Z0=-0 diverges (Zn2). With X being smaller and smaller we have:

Remainders theorem - E. Estenave - C. Frétigny

I can not put them all down, there's too many of them ! You will discover them as you read this page. Nevertheless here are a few examples:

and also:



...

Anonymous (see the attic)

From the sums of Riemann

         

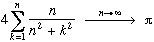
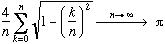
Triangle of c(n,k)

Some sums with factorials (see Gosper)

(1) from Euler and (2) from Comtet (1974)

Capes 1994 (an national exam in France to become teacher)

Let D be the disc of center z₀ and radius r :
D(z₀,r)={zC z-z₀r}
and r_k=min{r>0, z₀C, card(Z[i]D(z₀,r))k}

then

Chebyshev Polynômials

A first example :


If we know a relation of type : then we can construct the sequence U_n^k and the following sequence :
You want something different to 10 as the denominator? Sure, here is a even more general formula for p²>1, still starting from the relation with the Arctan :

with T(n,x) Chebyshev's polynomials.