c(n,k) Triangles

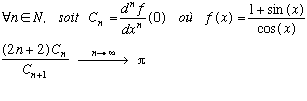
References taken from the Encyclopedia of Integer Sequences : A008280 - A008281 - A008282

Around

The above formula is the analytical expression of the c(n,k) definition.
(in this case, we have k=n)

But in 1966, Entringer was the first to make the following table which records the spread of the up-down permutation following the value of their first terms.
To make it, make the integer c(n,k) triangle, (0kn) in which each integer c(n,k) ( not to be confuse with combination (n choose k) ) is the sum of the last k terms from the n-1th line :

c(n,k)	k=0	1	2	3	4	5	6	7	8
n=0	1
1	0	1
2	0	1	1
3	0	1	2	2
4	0	2	4	5	5
5	0	5	10	14	16	16
6	0	16	32	46	56	61	61
7	0	61	122	178	224	256	272	272
8	0	272	544	800	1024	1202	1324	1385	1385

The numbers c_n seemed to have been known since Euler and comply to the definition at the top of the page.
In 1879, Désiré André has found the property to be also the number of up-down permutations of the interger 1 to n (this means that the n-1 successive difference between two consecutif terms of the permutation alternate between positive and negative.).
  For exemple, c₄=5 and we do have 5 up-down permutation of {1,2,3,4} :
1 3 2 41 4 2 32 3 1 42 4 1 33 4 1 2

For 1 3 2 4, we do have 3-1=2, 2-3=-1, 4-2=2

Notice that c_n=c(n,n). we then get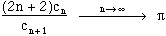

Method of prove

In fact, we can show that a power serie with general term gives /2 for convergence, (which seems logival if we consider the error bound in the Taylor expansion of the funtion f defined above)
Hence, the ration of the zⁿ coefficients must tend towards /2 according to Alembert's result.

Trials

The fraction give a near value of Pi by default if n is even and by excess otherwise :

n=0	1	2	3	4	5	6	7	8	9	10
2	4	3	3,2	3,125	3,147	3,1397	3,1422	3,14138	3,1416	3,141569

It seems to me that it converges logarithmiticaly, but I don't have the proof...