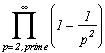Ernesto Cesàro
(1859 - 1906)

The probability that two integers ramdomly chosen are prime between them is ...
If we want to be able to use this result, we should reformulate it : If we choose two integers inferior to n , probability P that they are prime between them tends towards when n tends towards the

Slices of life

Cesàro was born in Naples in 1859. After studies in the school of the mines of Liege (Belgium), he teaches at the university of Naples (Italy) from 1883.
Being interested in arithmetic and series, he dies nevertheless prematurely by trying to save his son from the drowning...

About

A great result on Pi in the field of Probability! Because the condition of the theorem (2 random integers) can be applied in very different manners and there are many people that had brilliant or little serious ideas about it! For the relaxation, I advise you a small look on the column Attempts...

Proof

First of all, let us fix an integer n, as in the second formulation of the theorem.
We are going to make a little of enumeration by counting the number of couples (i, j) where i and j are inferior to n and prime between them...

1. First condition that they are prime between them is that they are not both multiple of 2. As a number out of two is multiple of 2 (!), the probability that i and j are divisible by 2 is 1/2*1/2=1/2 ² .
So the probability that i and j are not multiple of 2 is (1-1/2 ²).

2. Second condition is that i and j are not both multiple of 3. As well as previously, this probability is equal to (1-1/3 ²).
Well, that recalls me something!
As these conditions are independent, the probability that i and j are neither multiple of 2 nor 3 is (1-1/2²)(1-1/3²).
Now i and j will be prime between them if they are not both multiple of any integer, that is to say any prime number both, because any number is decomposable into first factors. By continuing for all the prime numbers the previous conditions, we obtain that probability P that i and j are prime between them is equal to, when n tends to the infinity:

But, but ! According to the section 4) of the part Proof of the Euler page, this means that looked probability is :

P =

All this is a little qualitative, but principle is especially important and demonstration can be made perfectly rigorously in the detail!

Trials

This result is especially important from arithmetical point of view, and, naturally, as usually in probability, convergence is extremely slow. We can not obtain in practice more than 5 decimals with this method... Nevertheless, let us run our imagination... Size in millimeter of a couple, the figures of a lottery, the decimal of a normal number are so many generators of couples of integers!
For example, R. Matthews used the coordinates of the 100 stars more bright of the vault of heaven... Here are couples of integers which gave him Pi=3,12772. It is exact to within 0,5% then... Would Pi be a hidden constituent of the universe?
By using the decimals of Pi in slices of 8 digits, J. Chuan obtained Pi=3,146634! Good heaven! Pi which gives Pi, it is extremely strong !
If you have other ideas, do not hesitate to inform us.