Kevin Brown's "Rounding Up"

So, lets take a natural integer n different from 0. For example 10. So far everything is all right !

Now let's considerthe nearest "multiple" bigger than or equal to n-1.

In our case, we find 18 because it is a "multiple" of 9=10-1 and bigger than 10.
Let us repeat this considering the nearest "multiple" bigger or equal to n-2, here 24, then of n-3 (28), of n-4 (30) and so on for n-k unto we get to k=n-1. We call f(n) the result (f(10)=34)
Well, funnily enough,

Erdös and Jabotinski proved that more precisely :

 

A second principle

In fact, Erdös and Jabotinski didn't use this construction that they didn't even mention; it seems to have been discovered by Kevin Brown.
They took a sort of riddle a bit like Eroatosthene's.
The sequel f(1) f(2) f(3)... can be constructed as follows :

Let's start from the sequel 1 2 3 4 5 6 7 8 9 10 11 12 13...
We take off one element on two starting with the third one (3).

So we keep
1 2 4 6 8 10 12 14 16 18 20 24 26 28 30 32 34...
We then take off one element on three starting with the fith :
1 2 4 6 10 12 16 18 22 24 28 30 34...
Then one element on four starting with the seventh :
1 2 4 6 10 12 18 22 24 30 34...
Then one element on five starting with the ninth :
1 2 4 6 10 12 18 22 30 34...
And so on taking off one element on (k+1) starting with the (2k+1)th element

However, I do not actually know if it was proved that it was the same sequel as above, or maybe it is obvious but I can't see it

K. Brown's preliminary constructions

The simplest thing is to take K.Brown's example again with the starting number n=100.
Here is a table where x represents the n-k and y the multiple bigger or equal to the previous n-k+1. It's what we did with x=9, y=18 then x=8 and y=24 and so on...

We will write w=y/x

   x   w    y       x   w    y       x   w    y       x    w   y


 100   1  100      75  26 1950      50  51 2550      25  122 3050
  99   2  198      74  27 1998      49  53 2597      24  128 3072
  98   3  294      73  28 2044      48  55 2640      23  134 3082
  97   4  388      72  29 2088      47  57 2679      22  141 3102
  96   5  480      71  30 2130      46  59 2714      21  148 3108
  95   6  570      70  31 2170      45  61 2745      20  156 3120
  94   7  658      69  32 2208      44  63 2772      19  165 3135
  93   8  744      68  33 2244      43  65 2795      18  175 3150
  92   9  828      67  34 2278      42  67 2814      17  186 3162
  91  10  910      66  35 2310      41  69 2829      16  198 3168
  90  11  990      65  36 2340      40  71 2840      15  212 3180
  89  12 1068      64  37 2368      39  73 2847      14  228 3192
  88  13 1144      63  38 2394      38  75 2850      13  246 3198
  87  14 1218      62  39 2418      37  78 2886      12  267 3204
  86  15 1290      61  40 2440      36  81 2916      11  292 3212
  85  16 1360      60  41 2460      35  84 2940      10  322 3220
  84  17 1428      59  42 2478      34  87 2958       9  358 3222
  83  18 1494      58  43 2494      33  90 2970       8  403 3224
  82  19 1558      57  44 2508      32  93 2976       7  461 3227
  81  20 1620      56  45 2520      31  96 2976       6  538 3228
  80  21 1680      55  46 2530      30 100 3000       5  646 3230
  79  22 1738      54  47 2538      29 104 3016       4  808 3232
  78  23 1794      53  48 2544      28 108 3024       3 1078 3234
  77  24 1848      52  49 2548      27 112 3024       2 1617 3234
  76  25 1900      51  50 2550      26 117 3042       1 3234 3234

You must read the table from x=100 towards x=1. The interval between two following y values gets smaller and smaller, but that is normal when you see y's construction. As long as it doesn't reach 0, w gets bigger, by one unit each time. As the interval between two y values gets smaller by 2 each time, obviously, this interval reaches 0 for x=50.
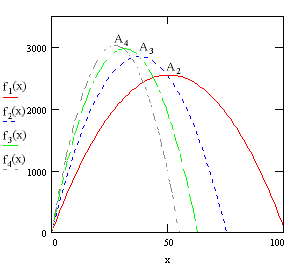
Up to this stage, we can modelize y by the f₁ parabola:

y=(101-x)x

Then, naturally, the interval beween two y values gets smaller by 4 each time, and so w gets bigger by 2 up to x=38. The model is then written as the f₂ parabola, whose equation is :

y=(151-2x)x

which reaches a maximum, and so its derivative is equal to 0, so the interval is equal to 0 with the previous one, for and that for the x integers
And in fact, from x=38, the interval between two following y values gets smaller by 6 each time, and w gets bigger by 3. y is then equal to :

y=(189-3x)x

which represents the f₃ parabola, and so on.
And so for the kth parabola, we can write :

y=(A_k-k.x)x

with A_k integer. If we derive to know the maximum of this parabola as we did previously, we get, for x :

(1)

To find the value of A_k, you just need to calculate the intersection point in between the k-th parabola and the previous one's maximum, which means :

(2)

We can see it on the following graph, where f₁, f₂, f₃... are respectively the parabolas of which we have calculated the equations :

we then replace y_k-1 by the value found in (1) and so we get :

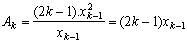
But then, with the A_k value found in (1), we can write :

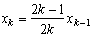
for k>1, because for k=1, we have :


Starting with x₀=y₀=n as we start from the integer considered at the beginning, we get :

When k approaches the infinite, y_k always reaches the f(n) value (as for n=100 for example, k can not go over 100)

To conclude, when n gets towards the infinite, we then get :

according to Wallis !

And that's another nice result.

Tests

Here is a calculation programme of the f(n) value in Maple. It is certainely not optimized, I just searched for a short and simple way to evaluate f(n) to do a few tests.

	brown := proc(n)
         local x,f,i,y;
             x := n;
             f := n;
             for i from x by -1 to 2 do
                 y := i-1; while y < f do  y := y+i-1 od; f := y
             od
         end

n=	n^2/f(n)=
10	2,94117
50	3,1172
100	3,0921459
200	3,14169
500	3,13999
1000	3,1390275

Well, seemingly it's an amusing series... In fact, if we actually get near Pi with n, some n values are favourable to the precision of the calculation, as n=200, and others aren't at all...Anyway, it seems to be a logarithmic convergence, like with Wallis' infinite product