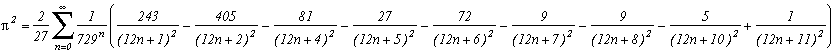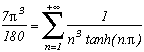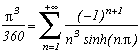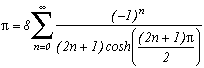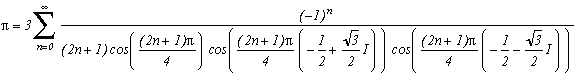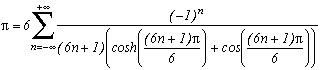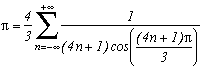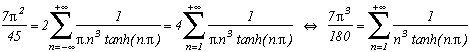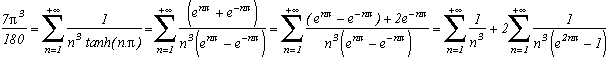Simon Plouffe / David Bailey
(To see more photos click on the one above)

Formulae derived from this

Adamchik-Wagon's formula

Other formulae :

Plouffe/Ramanujan/Borwein's identities on the (2n+1) (see Plouffe's page)

Original formula :



which gives us for example :






Other formulae of the same type from which we can get:

Slice of his life.

The best for David Bailey, is to see his personal site.
In brief, he did his phD in mathematics a the university of Stanford in 1976. He worked first in the departement of defence, then at Nasa, and now works in the laboratory Lawrence de Berkeley since 1998. He's a specialist in the detection of complete relation between numbers and of procedure of quick calculation.
As for Simon Plouffe, his site is also very instructif. He's a someone that is very kind and accesible, I can ssure you that it is always for me fascinating that I can sometime talk with such important people of the maths world without thinking to highly of myself. He passed his DEA (mastered in Canada) of maths under the direction of François Bergeron, who is now profesor at uqam. He then spend some years at the University of Bordeaux as a research assistant in the 80s, then joined uqam, more precisely the laboratoire de combinatoire et d'informatique (laboratory of combinatorial and computing), the LACIM.

Around

You might have already read the name Simon Plouffe without noticing... He was in the Guinness World Record Book in 1975 for managing to memorise 4096 decimals of... Pi (hey, how surprising!). After reaching 4400 and stopping, he continued his research on Pi until the 19/09/95, 0h29 where this famous and fabulous formula BBP (Bailey-Borwein-Plouffe) appeared to him on his computer...
Le fascinant nombre Pi by J.P. Delahaye (the fascinating number Pi) explain much better that I could here the relatively simple procedure where the congruences, euclidian divisions and Fast Fourier Transformation intervine so to allow to find in base 16, or more generally in base 2ⁿ, any "decimal" of Pi. (There are not decimals anymore, but digits...) So, if we imagine that we want to find the billionth digit in base 16, we just need to calculate the billionth digit of 1/(16ⁱ), which is simple with the congruence, and to skillfully manipulate the remainders that can appear in the a/(b+c*i) terms by calculating a few previous and later terms. I will be a bit more precise later on, promise....
Unfortunatly, a serie allowing to calculate the n-th digit in base 10 and quickly has still not been found... Notice to amateurs!
Plouffe developped with his usual trick a method that start from a serie that seems innocent, but whose complexity in O(n³log(n)) made it unusable in practise. Fabrice Bellard juste plunge in there and improved the algorithm in O(n²) but even with this, we are still far off from a formula that is really useful.

Proof

* Formula BBP

On the other hand, I won't deprive you of this wonderful proof for the formula BBP. It is surprisingly simple but imagining it must have been the hardest... :
First we calculate a little general result :

(The change sum-integral is completly justified since there's a uniformly convergence in the serie on [0,2^-1/2] )
So, if we apply this result on the serie BBP, we get :

we do a small change of variable y=2^1/2x to see a bit more what's happening...
= by decomposition into simple elements...
= with a bit of fiddling...
==


* For Plouffe's identies

Let us proof only the first identity, the others are of the same style :
Consider the function of the complex variable . According to the studies on the page Estenave/Frétigny, its integral on infinite square contours is nul, hence the sum of the remnant of this function is nul. Here is the table of the poles/remnants:

Poles	Remnants
0
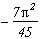
n
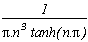
i.n
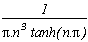
sum of the roots' remnants	0

So finnally we get :


to get the identity with (3), we cut the sum :

and there we go !
The whole point of this result, apart form the esthetic, come from the fact that we can accelerate the calculation of the decimals of (3). We do at the moment know more than 200 billion decimals of and all we need to fo is to calculate the precise value of exp() in the right hand side sum to be able to calculate the rest of the sum easily. Er get a linear convergence of roughly 2.72n which is really nice. Simon Plouffe assure us that he calculated in this way 30 000 and 50 000 decimals of (5) and (7) respectively. And several millions are possible, a really great trick in all!

The other formulae of the same type in cos and cosh come from the page on Estenave/Frétigny. They were also obtained from the theorem on remnants but in a different way, a bit more messy...

Trials

The formula BBP has not been made to calculate the decimals of Pi starting from the previous one, but let us procede to a few trial nevertheless... The shape itself comes directly from the perfomance of the little inequality written on the paragraph precision on the page dedicated to Machin.
Know that a precision of 2+log(8n)+n*log(16), which is good but not great :

n=1	3,14142 (3)
n=5	3,141592653228 (9)
n=10	15 correct decimals
n=50	64 correct decimals

Acceleration of the convergence

As we suspected after the mediocre performance on the sequence by Machin, the Delta2 of Aitken is not really useful here...

n=5	3,1415926535630
n=10	17 correct decimals

The number of decimals with which we can calculate Aitken's sequence is very high due to the sensitivity of th Delta2, hence we should push the serie BBP a few more extra terms...