|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
THE ATTIC
INTERESTING AND USELESS SEQUENCES...
A few sequences completly useless...
Using Riemann's method of sums :
(1)
(2)(3) 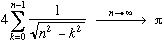
Little personal sequence found by my buddy David and I
(it is constructed by condering a circle where we inscribe verticle trapeziums. By calculating the the area of those trapeziums in a certain way, we stumble on the above sequence!)
Isolated sequence !
it's an archimedian sequence (polygons in a circle), prove later on!
Statistics/Counting
1) see Cesàro
2) c(n,k) triangles
3) Application of the law of large numbers
Letbe a random sequence of n points in the square [0,1]x[0,1] and Dn the size of the set of these points in the circle of center 0 and radius 1, i.e.
, then
.
A bit of geometry
The volume of a sphere in Rn is given by the formula:
where n=2m. Notice that this works really well for m=1, n=2 but it works as well for odd n ! In fact, for n=1, the length of the segment is 2R so :
And that's no joke! Recall that Euler's functioncheck that for integer n
(n)=(n-1)! and more generaly for positif real x,
(x)=(x-1)
(x-1)
Soaccording to the comment on the page about Euler and by condifering the function gamma as an extension of the factorial function on R+.
Try n=3, we do indeed get 4/3R3 !
Similarly, for the surfaces, we can consider that in dimension n, the volume of a sphere of radius R can be given according to its surface by :
which gives us :
What is more funny, is that those fomulae valid for all n can raide the following question: Does the volume and surface of a sphere have a maximum value for a given dimension ?
The answer seems to be yes in the sense that Vn and Sn tend to 0 if n tends to infinity (yes, the gamma function in n increase by a factor of (n-1)! and so a lot more faster than the power of the numerator).
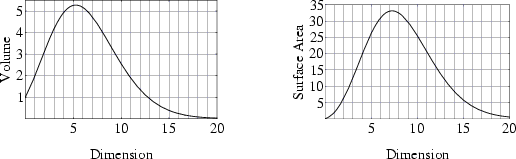
By deriving the expresions of Vn and Sn according to n, we find numericaly that the maximum value for the surface is in n=7,25695... and for the volume in n=5,25695... !
Therefor the sphere has a maximum value in dimension 5 and a maximum surface in dimension 7!
Underneath are shown the graphs of volume and surface in dimension n of those "hypersphere", borrowed from the fabulous encyclopedia by Eric Weisstein.
Seriously, this is serious...
Fagnano and the complex numbers.
We can have eternal fun with complex numbers... Apparently a certain Fagnano grant us the two following formulae :
Note anyway that by using the DLwith z being complexe with the second formula, we end up finding again :
which is no other than Leibniz's formula!
Pi and the euclidian spaces
During the external Cape maths challenge in 1994, dedicated to the study of the minimum radius of the disc from an euclidian plane containing k points to coordinates to integers, the candidates had to prove the following result :
Let D be the disc center z0 and radius r :
D(z0,r)={zC
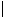
z-z0
r}
and rk=min{r>0,z0
C, card(Z[i]
D(z0,r))
k}
therefore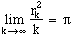
back to home page