Eugene Salamin / Richard Brent

Series inspired by Brent / Salamin's formula :

1) Original formula by Brent/Salamin on 1976 (Mathématics of computation )



2) Rather evident series that I did not strangely find anywhere!



3) Variation of the Borwein brothers on 1984



4) Borwein brothers on 1987 ( Pi and the AGM )

Another series according to Salamin's observation

I have not yet tested these algorithms.

Quadratic convergence


Cubic convergence

This algorithm converges towards the closest multiple of Pi of f₀.

f_n=f_n-1+sin(f_n-1)

I did not regrettably find the proof of these algorithms...

Slices of life

And I did not find a lot about Salamin or very little... As this picture showing him together with the greatest researchers on Pi (Bailey, Gosper, Kanada...)
About Brent, on the other hand, all is OK ! Richard Brent is an autralian mathematician who was born in 1946. He is currently a professor at Oxford and is a specialist of the algorithms. For more informations, you can go to visit his personal page.

About

The original formula was discovered in 1973 and published in 1976 by Eugene Salamin in the article Computation of Pi in the magazine Mathematics of computation . It was published at the same moment and independantly by Richard Brent ( Who is now moreover manager of Mathematics of computation !). It is true that the habit is to call it Salamin's algorithm, but let us not forget this dear Brent !
This formula is the first real important discovery concerning the computation of Pi since the formulae of arctan and thoses of Ramanujan. The strength of this algorithme is to propose a quadratic convergence (2ⁿ as I used to note it on this site) that is to say that the number of correct decimals doubles on every iteration ! A rocket !
Of course, the proof is as hight as the performance, as the very painful length... But I spent such a time vainly on the internet in search of this proof when I needed it for my file about Pi (see page perso) that I can resist to publish it there...
It is based on the arithmetico-geometrical mean that was studied by Legendre and Gauss, but this last one, for onse (!), did not see the interst that it could have for the computation of Pi !

Proof

Let us go for algorithms 1) 2) and 4)! I am going to tempt to well structure the posting of the results because the web is not the more convenient for the mathematical prooves!

Arithmetico-geometrical mean

let a and b two positive or nil reals. We define series (a_n) and (b_n) by :

I Convergence

Lemma 1 : (an) and (bn) are convergent and of the same limit. Furthermore, (an) is decreasing and (bn) is increasing. This limit is noted M(a,b) and called arithmetico-geometrical mean of a and b.

Proof

I.a) Let us prove that for n>0 and a#b,

• In fact, if a=b, one immediately obtains for every integer n that a_n=a=b_n
  
  
• If a=0 or b=0, one has (immediately again !) for every integer n b_n=0 and a_n+1=a_n/2 that well proves (1) and (2)
  
  
• If a>0 and b>0, a#b

I.a).(1) A small recurrence for (1) to begin well !
n=1 : a#b so by developping, so b₁<a₁, and by redoing the same, b₂<a₂.
Moreover, a₂=a₁ /2+b₁ /2<a₁ /2+a₁ /2=a₁ so a₂<a₁ and b₂>(b₁²)^1/2=b₁ so, finally, one has the result (1) at the rank 1

Let us suppose now that result (1) is true for k in [[1,n]]...
Since b_n<a_n, one has again (a_nb_n)^1/2<(a_n+b_n)/2 so b_n+1<a_n+1 and a_n+1<2a_n/2=a_n and finally b_n+1>(b_n²)^1/2=b_n
So 0<b_n<b_n+1<a_n+1<a_n
This is realy the hypothesis at the following rank, so by the recurrence theorem, the result (1) is correct for every integer n not nil...

I.a).(2) Pour tout n>0, on a :

That is well the result (2) !

---

I.b) Let us show now that these series are convergent :

• If a=b one hase for every n a_n=b_n ans so (difficult !) a_n=a=b_n
• If b=0, a#0 one has fir every n>0 : b_n=0 and a_n=a_n-1 /2=a₀ /2ⁿ so a_n=b_n=0
• If a=0, a_n=0 and so b_n=0 for every n, that solves the problem of the limit !
• If a>0, b>0, a#b
  _ According to I a) (1) (b_n) is increasing, and (a_n) is decreasing
  _ Moreover, according to I a) (2) and by an immediate recurrence, a_n-b_n<(a₁-b₁)/2^n-1 so (a_n-b_n)=0, hullo !
  Would not it be adjacent series ? Of course yes ! So they converge toward a same limit that we will note M(a,b)

---

II Properties of the arithmetico-geometrical mean AGM

II.a)  M(an,bn)=M(a,b) II.b)  M(a,b)=M(b,a) II.c)  M(ßa,ßb)=ßM(a,b) for every integer n, ß>0, a>0, b>0

Proof

II.a) Given n₀>0
(a_no+k)_k and (b_no+k)_k got same limit that (a_k)_k and (b_k)_k so, M(a_no,b_no)=M(a,b)

II.b) Given (a'_n) and (b'_n) the series defined by (a_n) and (b_n), but with a'₀=b and b'₀=a
One has a'₁=a₁ and b'₁=b₁ so according to I. a) with n=1, one has M(a,b)=M(b,a)

II.c) Also, if one defines (a"_n) and (b"_n) by a"₀=ßa₀ and b"₀=ßb₀, one has immediately for every n : a"_n=ßa_n and b"_n=ßb_n.
So, at the limit one has, M(ßa,ßb)=ßM(a,b)

---

III Function f(x)=M(1,x)

Here we are in the heart of the proof : for a=1 and b=x, the previous results (convergence...) allow us to build a function f defined by :
For x positive or nil real,

f(x)=M(1,x)

The interesting results on this function are :

III.a) Lemma 2

f is continuous on [0,+[

Proof

In the case a₀=a=1 and b₀=b=x, we will show that the uniform convergence of the series (a_n) and (b_n) on every compact of R⁺ toward the function f. To well differentiate this case of the previous study, I will note respectively (U_n) and (V_n) these series of functions...

III.a).1) Let us show that for every integer n, U_n and V_n are continuous on R⁺

By recurrence, for example !
n=0 : U₀(x)=1, V₀(x)=x, no comment !
Let us suppose the result until a certain integer n,
U_n+1=(U_n+V_n)/2 and V_n+1=(U_nV_n)^1/2 so U_n+1 and V_n+1 are clearly continuous as composition of continuous functions...
The recurrence theorem is verified, U_n and V_n are continuous for every n on R⁺.

---

III.a).2) Let us show the uniform convergence of U_n and V_n toward f on every compact of R⁺ :

• According to I.a).1). one has n0, b_nM(a,b)a_n so :
• xR⁺, V_n(x)f(x)U_n(x) so :
  
  0U_n(x)-f(x)U_n(x)-V_n(x)<(U_n-1(x)-V_n-1(x))/2<|1-x|.2^-n for every xR⁺
  
  
• Let us place on a compact [A,B] of R⁺
  nN*, 0U_n(x)-f(x)(B+1)2^-n
  
  Also, 0f(x)-V_n(x)U_n(x)-V_n(x)<|1-x|2^-n(B+1).2^-n

This upper bounding is uniform, so there is uniform convergence of (U_n) and (V_n) toward the function f on every compact of R⁺

So f is countinuous on [0,+[, it's already a very important result !

---

III.b) Lemma 3

f is increasing on [0,+[

Proof

III.b).1) Let us show by a recurrence (again!) on nN that (Un) and (Vn) are increasing on [0,+[
U₀=1 and V₀=x so one has the result for n=0
Let us suppose that the result is true for a certain nN
U_n and V_n being increasing, U_n+V_n and also(U_nV_n)^1/2 so U_n+1 and V_n+1 are also increasing and this is the hypothesis at the following rank !
The result is true for every nN.

---

III.b).2). Given x₁0, x₂0 with x₁<x₂
Since there is uniform convergence of (U_n) towards f, one has f(x₂)-f(x₁)=(U_n(x₂)-U_n(x₁))
now nN*, U_n(x₂)-U_n(x₁)0 (growth of U_n), so f(x₂)-f(x₁)0, that insure us of the growth of f on [0,+[, and so, this is the end of the proof of lemma 3 !

---

III.c) Lemma 4 (Study at bounds...)

f admits a vertical tangent in x=0 In 0, lim f =0 In +, lim f =+ , f(x)=o(x)

Proof

III.c).1) one has x^1/2=V₁(x)f(x) xR^+*, so x^-1/2f(x)/x and finally :

so f admit a vertical tangent in x=0.
If x=0, for n1 U_n(x)=U_n-1(x)/2=2^-n, and V_n(x)=0 so f(0)=0

---

III.c).2) According to II.b) et II.c),
xR^+*, f(x)=M(1,x)=xM(1/x,1)=xM(1,1/x)=xf(1/x)

When x -> + lim f(1/x)=f(0)=0 because f is continuous in 0
so f(x)/x->0 and in +, f(x)=o(x)

Moreover xR^+*, f(x)x^1/2, so in +, lim f=+

---

III.d) Theorem 5

f is C class on ]0,+[

This result is very strong (almost too, since we will only need of the character C¹!) is not simple to proove. It will even drive us to the theory of elliptic integrals !
So, we will successively :
III.d).1) Express M(a,b) by an elliptic integral I(a,b)
III.d).2) Apply this result to function f
III.d).3) Use the character C of I(1,x) to deduct the one of f !

Proof

III.d).1) We will take an interest in the following integral,
Given a,b>0, let pose :

III.d).1).i) Convergence

Given and m(0)=1/(ab), now m being of course continuous on R⁺, m is integrable on R⁺ and so I(a,b) is well defined...

---

III.d).1).ii) Change of variable

Let us pose
this is a increasing bijection so let us do a little change of variable... Let us pose t=b.tan(y), one obtains :

---

III.d).1).iii) function g

One defines the function g by g(x)=I(1,x)

Let us show that it is C class on ]0,+[

Given h(x,y)= with (x,y)]0,+[*[0,/2]

Let us show by a recurrence on nN (allways !) that exists ans is continuous on ]0,+[*[0,/2]
In this way, let us show in the same time, allways by recurrence, that with the hypothesis on parameters :

(x,y)= where x -> P_n(x,y)R_n[x]

• n=0, this is the definition of h !
  h is clearly continuous on ]0,+[*[0,/2] and admit a partial derivative in x
• n=1 :
  This is truly the foretelled form for n=1 and this is perfectly continuous on ]0,+[*[0,/2]
• Let us suppose now the result for a certain nN
  
  that is truly the waited result with P_n+1 of the wanted form... P_n+1 is a polynomial in x and a trigonometrical polynomial in y and is so therefore continuous on ]0,+[*[0,/2] and derivable in x. As for the denominator, the hypothesis of recurrence is verified at rank n+1, that concludes the recurrence !

h is C on ]0,+[*[0,/2]

Since we are on the segment [0,/2] for y, the function g defined by :

g(x)=h(x,y)dy

is C on R^+* and one has :

g⁽ⁿ⁾(x)=(x,y)dy

x -> I(1,x) is a C function on R^+*

Now we have to express M(a,b) in function of I(a,b)

This is, of course, the main result of this study and it was obtained by Gauss (he did not go farer !).

---

III.d).1).iv) First of all let us show that :

=I (a,b)

In that way, let us pose j(t)= defied on R^+* and that is clearly a bijection from R^+* to R ( j'(t)=>0 ) so, in I(1,t) defined at 1), one poses s= and one obtains :

and on the other hand, ds=dt, so one obtain finally :

The last but one equality being obtained thank to the parity of the term under the integral

---

III.d).1).v) So, let us show now that
One has clearly I(ßa,ßb)=I(a,b)/ß so :



now a_n=M(a,b) and one has a_n/b_n=1.
Moreover, g is continuous on R^+* according to iii) so :

that allow us to conclude :

---

III.d).2) by applying this result to the function f, one obtains

---

III.d).3) And the proof of the theorem 5 is finished, g being C on R^+*, f also on the same interval

Small note : f is continuous in 0 but is not differentiable in 0 according to lemma 4...

---

III.e) Asymptotic attitude of f

We will search for equivalent of f at the bounds of R⁺ thank to equivalents of g

Lemma 6

Proof

III.e).1) A new expression of g !

Let us pose haphazardly (!) s=x/t :

---

III.e).2) Let us find now an equivalent of g in the neighbourhood of 0

t[0,x^1/2], one has 11+t²1+x, so




so according to III.d).2) one has :

the second equivalence being coarsly obtained thank to III.c).2) (f(x)=x.f(1/x))

---

IV Expression of Pi in function of f and f'

We will show that =

In that way, we restrain U_n and V_n to ]0,1[ and we introducet W_n and k_n, function defined on ]0,1[ by :

W_n= and k_n=

These functions are obviously well defined and positive because according to III a)2) 0<V_n(x)<U_n(x) on ]0,1[

---

IV.a) Convergence of (k_n)_n

IV.a).1) Properties

2M(Un+1,Wn+1)=M(Un,Wn)

Proof



Let us pose a=U_n+V_n=a₀, b=U_n-V_n=b₀ as at I, one has

---

IV.a).2) Convergence

Proof

---

Proof



so according to the asymptotic study of III e), one obtains :

according to the previous property, that allow us to conlude :

strong !

---

IV.b) Convergence of (k'_n)_n

Let us be interested in the derivative series of functions (k'_n)_n. In fact, f' appears in the final searched expression , so there is great chances that we speack of derivatives series at a moment... so that is become clear :

IV.b).1) Existence et positivity

nN, Un, Vn, Wn, kn are continuously derivable Moreover, x]0,1[, nN*, U'n>0, V'n>0

As for the continuity of U_n and V_n, we do a recurrence on n to prove that. So let us be brief !
U₁ and V₁ obviously verify the property and if we suppose that the property is true for a certain rank n, a small calculus according to the definition of U_n and V_n gives us
that insure the existence, the continuity and the positivity at rank n+1... Hop, this is finished, needless to waste time on such recurrences !

W_n and k_n being composition of continuously derivable functions, they are also for every n...

---

IV.b).2) Expression of (k'_n)

x]0,1[, nN,

Proof :

according to IV a)1) so



now V_n²=U_n²-W_n² and if we derive, 2V_nV_n'=2U_nU_n'-2W_nW_n' so :



and one finally obtains :

---

IV.b).3) Convergence

(k'n) uniformly converges on every compact of ]0,1[ towards : x->

Proof

Let us set on [a,b] compact of ]0,1[, 0<a<b<1
nN, x[a,b], one has :


by using III.a).2)...

This upper bounding involves the uniform convergence of (k'_n)_n towards
x -> on every compact of ]0,1[

---

IV.c) Expression of Pi

Here we are, finally !

IV.c).1) Dérivative

x -> is the derivative of x ->

Proof

• nN, k_n is C¹ class on ]0,1[ according to IV b)1)
• the series of function (k_n)simply converges on ]0,1[ towards the function
  x-> according to IV a)2)
• The series of functions (k'_n) uniformly converges on every compact of ]0,1[ towards x ->

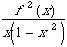
So by applying the theorem of derivation of the series of functions,
x-> is the derivative on ]0,1[ of x ->

---

IV.c).2) Différential equations

f verifies the differential equation : x]0,1[,

Proof

Easy ! We simply have to derive x -> and to use the previous result a).
I do not do that, that is only calculus !

---

IV.c).3) Expression of Pi

The quest of the mathematical Holy Graal would go to his end ? Anyway, we touch here the most important result of the proof !

=

Reference from the Encyclopedia of Integer Sequences about M(1,sqrt(2)) : A003054


Proof

Easy again ! We just have to pose x= in the diiferential equation. As previously, that is only calculus. I will not overload this page with useless expressions.

That is a great result !
And it will be the fundation of many very efficient algorithms with a quadratic convergence

---

V Applications


Serious things now !
Many uses on this formula are possible :

V.a) Direct use of derivative series

The first thing of that we think is to use the derivative series (U'_n) and (V'_n) converge towards f' (the proof of this convergence is given at V.b) ). One obtains replacing f and f' by U_n and V_n of different ways the following algorithm :

Even if it seems more complicated than the algorithms of Borwein or Brent/Salamin, I was amazed to not find it anywhere ! But in my concern of exhaustiveness, I could not miss to notice it.

---

V.b) Algorithm of J. and P. BORWEIN (1987)

This algorithm was published in Pi and the AGM. I will give the detailed proof and by estimating the efficiencecy... It is given under the form :

Proof

We will set us during all the proof on a compact K of ]0,1[
With the notations of the previous parts, let us pose for n1 :

V.b).1) Convergence

Let us show that :

yn1, zn1, nN* (yn) and (zn) uniformly converge towards 1 on K

Proof

* According to III.a).2). and the definition of y_n and z_n, U_nV_n, so y_n1
* nN, x]0,1[

according to III.a).2). and V_n(x)>V₀(x)=x.
On K, one has x->1/x-1 is bounded (continuous on a compact) by a certain MR^+*, so

xK, y_n(x)-1<M.2^-n

by this way, (y_n) uniformly converges towards 1 on K

* Let us show by a recurrence on nN* that z_n1

n=1 : z₁=x^-1/2>1 on ]0,1[
Let us suppose the result for a certain nN*

that show us the relations of recurrence for (y_n) and (z_n) !
so

because z_n1 by the hypothesis of recurrence and y_n1 according to previously, in consequence this ends the recurrence...

For n1, z_n+1-y_n+1 is of the sign of :
2(1+y_nz_n)-(1+z_n)(1+y_n)=1+y_nz_n-z_n-y_n=(z_n-1)(y_n-1)0
so

z_n+1y_n+1

z_n+1-y_n^1/2 is also af the sign of :
1+y_nz_n-y_n(1+z_n)=1-y_n0
now y_n1 so y_n^1/2y_n and finally :

y_n+1z_n+1y_n^1/2y_n

so 0<y_n+1-1<z_n+1-1<y_n-1 and :

Sup_K(z_n+1(x)-1)Sup_K(y_n(x)-1)

The uniform convergence of (y_n) towards 1 on K insures, by this way, the uniform convergence of (z_n) towards 1 on K...

---

V.b).2) Let us show now that (U'_n) and (V'_n) uniformly converge on K. This is certainly the hardiest to obtain, but it works and it is the main thing !!

Given x]0,1[, nN*,
z_n1, so U'_nV'_n and as U'_n+1=(U'_n+V'_n)/2 one has U'_n+1U'_n
so (U'_n) is increasing
V'_n+1(x)-V'_n(x)= so te sign of V'_n+1(x)-V'_n(x) is the one of :
.

By dividing by U'_n(x)V'_n(x)>0 one obtains :


now, according to a), y_n^1/2-1y_n-1z_n-1, and (z_n) uniformly converge towards 1 on K so at a certain rank n₀, for nn₀,
xK, 0<z_n(x)-1<1/2, so :

because z_n(x)2

so for nn₀ and xK, V'_n+1(x)V'_n(x) and finally :

U'_n(x)U'_n+1(x)V'_n+1(x)V'_n(x)

This being, given ß>0
(z_n) uniformly converges towards 1 on K, so it exists n₁N such that :

nn₁ => 0sup_K(z_n(x)-1)<ß*V_no(x)^-1

now
with nMax(n₀,n₁) and since (V'_n) is decreasing according to above (eh yes!), one has for nMax(n₀,n₁) V'_n(x)V'_no(x), so :

0V'_n(x)-U'_n(x)<ßV'_no(x)V'_no(x)^-1=ß

x]0,1[, (U'_n(x) and (V'_n(x)) are adjacent series and converge towards the same limit that we will note µ(x).
So one has :

x]0,1[, 0U'_n(x)U'_n+1(x)µ(x)V'_n+1(x)V'_n(x)

For nMax(n₀,n₁) one has :

x]0,1[, 0µ(x)-U'_n(x)V'_n(x)-µ(x)ß

So the series (U'_n) and (V'_n) uniformly converge on K towards µ(x)

V.b).3) Let us build the series (f_n) (finally !)

(U_n) uniformly converges (so simply) on K towards f and (U'_n) uniformly converges on K so his limit is f' on ]0,1[

Let us pose

One has :

then

that concludes the proof. Ah ! what a beautiful result !

Performance

The length of the proof of the XXe century has is award at the chapter of performances.
This algorithm is in fact a quadratic convergence. That is to say that the number of decimals true boubles on each iterations, but we can not see that at the first view !

Let us show that :

Proof

Given nN.


For x=2^-1/2, a small numerical calculus gives us :

On the other hand,


Now, one has , the terms ellimate them eachother. So we do k tends towards +, and one obtains :

---

V.c) Algorithm of Brent/Salamin (1976)

The original algorithm is this one, we can not go on his proof, which I did not find anywhere, but it is not difficult to do it thanks to the work done previously !

This algorithm is given under the form :



Proof

It is quick ! Let us take the previous notations back...

V.c).1) Remember that : k_n=
now W_n= so


now according to IV.b).2), on ]0,1[ by a consequence

in x=2^-1/2

V.c).2) On the other hand let us pose


let us calculated (again !) :
(hullo !)



By an immediate recurrence, one has :

by simplifying the notations.

So, one finally obtains:



That concludes all the part of the proof and allow me to rest a little (Ouf ! this page was so long...)

---

Trials

The series presented have similar performances. For example, concerning the second one (Borwein), to obtain 10 000 000 of decimals of Pi, we just have to have n19 !

The trials are rather amazing :

n=	1	2	3	4	5	6	7	8	9	10
d=	2	8	18	40	83	170	344	693	1392	2789

d is the mumber of right decimals of Pi
The quadratic convergence is perfectly respected, that is to say that the number of decimals bouble on each iteration.

Moreover, the time of calcul of n decimals, that requires for the classical methods a time proportional to n², is reduced at about n.Log(n) with the algorithms of Brent/Salamin and Borwein... A small revolution !