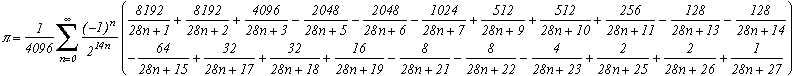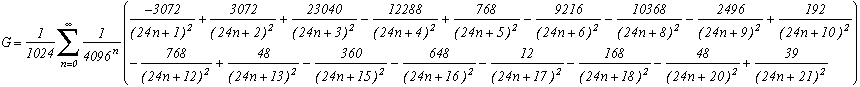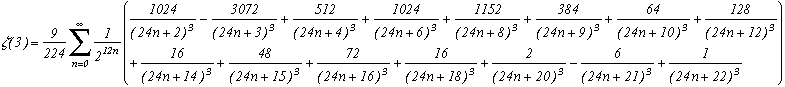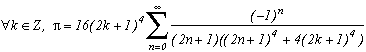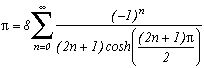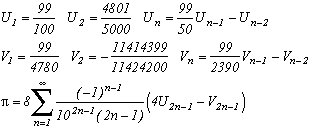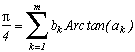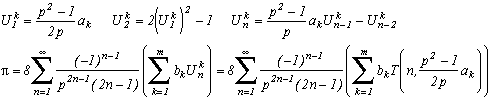Quelques idées personnelles
de formules

version PDF

Depuis que je m'intéresse au nombre Pi, j'ai souvent caressé l'espoir de découvrir une propriété mathématique sur ce nombre, ou même un autre, qui n'aurait pas été découverte. Evidemment, je ne m'appelle pas Euler et à mon niveau, en tant qu'étudiant en statistiques, il est bien difficile d'être efficace. Les mathématiques ne restent souvent pour moi qu'un rêve. Néanmoins, j'ai parfois quelques idées dont je ne sais pas trop ce qu'elles valent, mais ça ne m'empêche pas d'essayer de les exploiter ! Et plusieurs internautes m'ont aussi aiguillé vers des domaines bien intéressants qui permettent, au terme de collaborations plus que fructueuses et très instructives pour moi, d'en sortir de jolies formules.
Témoin les expressions qui suivent, je ne sais pas si elles sont connues, je ne pense pas d'ailleurs pour certaines d'entre elles ! Si vous vous intéressez un peu aux mathématiques sous-jacentes vous serez , j'espère, amené à les apprécier, à les critiquer (!), à me dire si vous avez d'autres idées, etc...
Enfin voilà, assez parlé, je vous laisse découvrir ces modestes contributions...

De nouvelles formules BBP très rapides pour diverses constantes

Pi=



et plus généralement


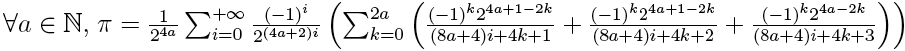
(merci à D. Wolf pour l'erreur détectée). Cette formule n'est pas encore démontrée.
(j'en mettrai ici d'autres prochainement, j'en ai toute une cargaison, mais il faut les mettre en forme !)


Constante de Catalan=G



Cette formule est maintenant démontrée. La preuve sera disponible prochainement.

Zêta(3)=(3)



(Ca, c'est tout de même ma préférée, car à ma connaissance, après avoir bien cherché, on ne connaissait absolument pas de formules BBP pour calculer Zêta(3), et elle permet en outre un calcul rapide des décimales !)

La démonstration de la formule précédente est expliquée dans le fichier au format pdf/ps suivant (C'est une histoire un peu compliquée de polylogarithmes...) :
format pdf
format ps

Diverses autres contributions

Elles sont déjà présentes sur le site sans que vous les ayez peut-être remarquées !

1) Il y a bien évidemment ma formule de jeunesse :

dont j'ai appris qu'elle était connue au début des années 90, ce qui ne m'a guère étonné vu sa simplicité ! Mais j'ai une tendresse particulière pour elle car elle date de l'époque héroïque où mon ami David et moi-même (16 ans alors et seulement le bac en poche) avions décidé après sa découverte de faire une synthèse des suites convergeant vers Pi. Et c'est ainsi que tout a commencé !!
(elle se construit en considérant un cercle où l'on inscrit des trapèzes verticaux. En calculant l'aire de ces trapèzes d'une certaine manière, on tombe sur la suite que voilà !)

2) Ma collaboration avec Christian Frétigny de la prestigieuse ESPCI a permis, sur son idée, de réaliser une petite classification des diverses sommes d'un type donné obtenues à l'aide du théorème des résidus.
Par exemple :

ou bien

Vous pouvez retrouver cette exploration à la page :
Estenave/Fretigny

3) Enfin, une petite idée anodine un soir, et hop ! Voilà un algorithme convergeant vers Pi, simple à mettre en oeuvre, à démontrer, et ressemblant étrangement aux séries BBP :

et plus généralement, si :

alors

pour p²>1 et avec T(n,x) le polynôme de Chebyshev.
Vous pouvez retrouver cet algorithme sur la page :
Chebyshev