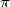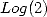|
|
|
|
|

Benoit Cloitre
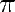 et
et 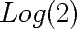 dans un miroir
dans un miroir
Benoit Cloitre, toujours aussi imaginatif, poursuit sa chronique des similitudes entre constantes célèbres
après celle entre  et
et 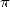 .
.
1 Pour 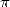
Soit
Soit 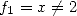 et
et 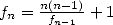 alors
alors 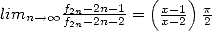 . En conséquence, si l’on
écrit
. En conséquence, si l’on
écrit
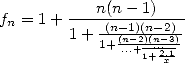
alors on obtient une fraction continue type Brounker inversée.
2 Pour 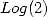
Soit 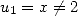 et
et 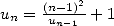 alors
alors 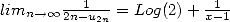 . La fraction continue
équivalente est
. La fraction continue
équivalente est
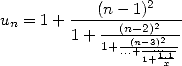
Preuve pour Pi
Il est aisé de voir que, par induction, 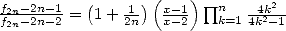 et l’on reconnaît le produit de
Wallis .
et l’on reconnaît le produit de
Wallis .
Preuve pour 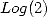
Soit 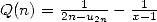 . On voit facilement que pour
. On voit facilement que pour 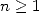 ,
,
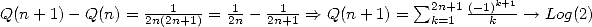 .
.
Vérification par code Pari-GP
Pour Pi
-
x=171679;u=x;for(n=2,100,u=n*(n-1)/u+1;if(n%2==0,print1((u-n-1)/(u-n)-prod(k=1,n/2,4*k^2/(4*k^2-1))*(1+1/n)*(x-1)/(x-2),",")))
,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
Pour log(2)
-
f(n)=if(n<2,171679,(n-1)^2/f(n-1)+1);Q(n)=1/(2*n-f(2*n))-1/(171679-1);for(n=1,10,print1(Q(n+1)-sum(k=1,2*n+1,(-1)^(k+1)/k),","))
0,0,0,0,0,0,0,0,0,0,
Retour à la page d'accueil