|
|
|
|
|

Benoit Cloitre
e et
dans un miroir
Benoit Cloitre est un brillant amateur de mathématiques à ses heures.
On considère les suites
![]() n et
n et ![]() n définies par
n définies par
u1= 0, u2 = 1, un+2 = un+1 + 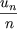 |
v1= 0, v2 = 1, vn+2 = 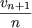 + vn + vn |
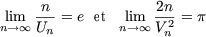
Plus généralement, on a
u1= x, u2 = y, un+2 = un+1 + 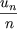 |
Alors
lim n![]()
![]()
![]() = x +
= x + ![]()
En considérant
ces deux séquences, e et  sont comme dans un miroir ! Cependant, les vitesses de convergence sont très différentes...
Un converge
très rapidement (de plus en plus vite) tandis que V n converge
de manière logarithmique...
sont comme dans un miroir ! Cependant, les vitesses de convergence sont très différentes...
Un converge
très rapidement (de plus en plus vite) tandis que V n converge
de manière logarithmique...
Benoit Cloitre a proposé originellement une preuve directe, mais l'on peut préférer celle de Gery Huvent, de Lille, qui permet de proposer une méthode générale de démonstration pour ces suites.
2.1 PourUn calcul des
premiers termes 0,1,1,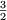 ,
,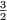 ,
,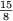 ,
,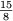 laisse
suggérer que
laisse
suggérer que
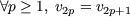
Cette propriété se prouve par récurrence sur p, en effet c'est vrai pour p = 1. Supposons que v2p = v2p+1 alors
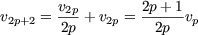
et
| v2p+3 | = 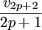 + v2p+1 = + v2p+1 = 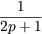 * * 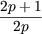 vp + v2p vp + v2p |
= 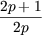 vp = v2p+2 vp = v2p+2 |
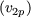 p vérifie
p vérifie
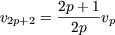
ce qui donne par récurrence
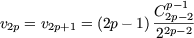
Compte tenu de l'équivalent classique (obtenu classiquement avec Wallis)
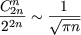
on a
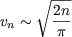
Remarque On peut donner un développement limité avec la formule de Stirling, pour obtenir
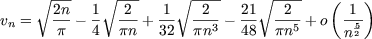
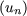 n
n
Considèrons
la fonction génératrice de la suite 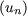 n
n
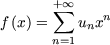
la récurrence donnée se traduit par
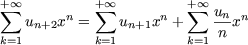
soit
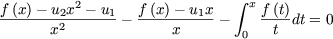
en dérivant, on obtient
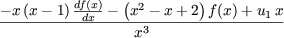 = 0
= 0
ainsi f est solution de l'équation différentielle
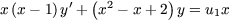
dont la solution générale est
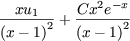
compte tenu de
u1 = 0 et de
u2 = 1 = 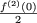 on
trouve
on
trouve
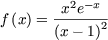
Il s'agit maintenant de déterminer le développement en série entières de f afin de récupérer les termes de la suite. Pour cela on remarque que
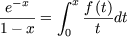
( 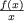 = v2x + v3x2 + ....est définie
en 0 )
= v2x + v3x2 + ....est définie
en 0 )
Ensuite, on se souvient que si
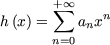
alors
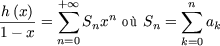
d'après le produit de Cauchy de deux séries. Ainsi
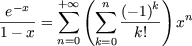
et
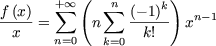
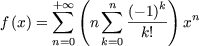
et
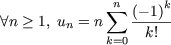
en particulier
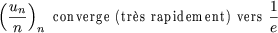
Remarque Si on opère de même avec la suite 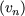 n, la fonction génératrice est
solution de
n, la fonction génératrice est
solution de
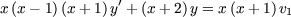
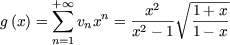
qui vérifie
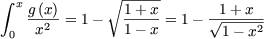
avec
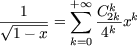
retour à la page d'accueil
