|
|
|
|
|
Algorithmes à convergence ultra-rapide !
Basés sur la théorie des équations modulaires ou sur la moyenne arithmético-géométrique
(XXe siècle)
1976 :
variante facile à construire :
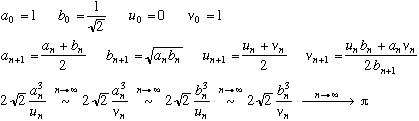
Je n'ai pas encore testé les algorithmes qui suivent.
Convergence quadratique
Convergence cubique
Cet algorithme converge vers le plus proche multiple de Pi de f0.
fn=fn-1+sin(fn-1)
1) 1984 : convergence quadratique (reposant sur la moyenne arithmético-géométrique)
2) 1987 : convergence quadratique (reposant aussi sur l'AGM)
3) convergence quadratique (reposant sur les équations modulaires comme les suivantes)
4) convergence quadratique :
5) convergence cubique :
6) convergence quartique :
7) convergence quintique :
8) convergence septique :
9) convergence nonique :
10) convergence "hexadécimalique" ! (ordre 16)
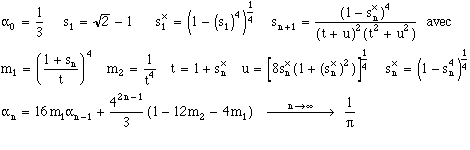
retour page d'accueil
