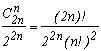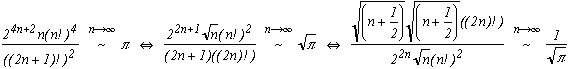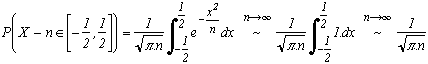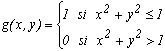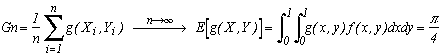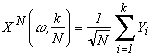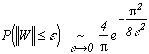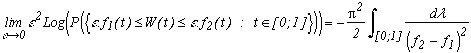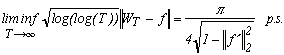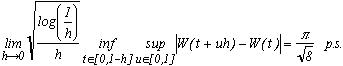Les apparitions de Pi dans les phénomènes aléatoires

Cette page est une des trois consacrées aux relations pour le moins complexes entre notre constante Pi et le domaine de l'aléatoire. Ce dernier ne pouvait se contenter d'une page car sa consistance est assez épaisse et il recèle plusieurs approches qu'il n'est pas toujours simple d'expliquer en deux mots !
Cette page s'enrichira au fil de ma collecte, elle n'est pour l'instant qu'une introduction, car il y a beaucoup trop de choses à dire pour pouvoir s'en sortir en une seule fois !
Et je n'ai pas vraiment trouvé toutes les démonstrations, si vous en voyez, prévenez-moi...

Voici les paragraphes abordés successivement :

A - Pi et les théorèmes liés aux probabilités

1 - Cesàro
2 - Buffon
3 - Jeu du Pile ou Face
4 - Monte-Carlo

B - Pi et les processus aléatoires

1 - Quelques notions sur le Mouvement Brownien
2 - Les probabilités asymptotiques de petite boule brownienne
3 - Les lois limites presque sûres
4 - Temps d'occupation de R⁺ par W sur [0;1]

et deux trois éléments de Bibliographie

---

A - Pi et les théorèmes liés aux probabilités

Pi apparaît dans de nombreux théorèmes un peu isolés, et que l'on considère souvent comme relevant du domaine des probabilités. Moi, j'appellerais cela des probas de loto (!), car on est souvent plus dans des questions de proportions, de dénombrement, et d'aires que des véritables théorèmes de probabilité relevant de la théorie de la mesure sous-jacente !
Cependant, ces résultats sont assez fascinants et amènent Pi là où l'on ne s'attendrait pas du tout à le voir apparaitre !
Les plus célèbres sont sans aucun doute les théorèmes de Cesàro et Buffon dont voici les intitulés, et qui ne sont pas neufs pour les habitués du site :

Théorème de Cesàro

La probabilité que deux entiers choisis au hasard soient premiers entre eux est ...
Si l'on veut pouvoir utiliser ce résultat, il convient de reformuler car le nombre de couples d'entiers est infini : Si l'on choisit deux entiers inférieurs à n, la probabilité P_n qu'ils soient premier entre eux tend vers lorsque n tend vers l'infini.

La démonstration est disponible sur la page consacrée à Cesàro

Théorème de l'aiguille de Buffon

Si on laisse tomber une aiguille de longueur 2a sur un parquet formé de lames de largeur 2b, la probabilité pour que l'aiguille coupe l'une des raies de ce parquet est




La démonstration est disponible sur la page consacrée à Buffon.

Jeu du Pile ou Face

Lançons 2n fois une pièce de monnaie, vous en avez bien une petite qui traine ? Le nombre de cas possibles, puisqu'il n'y a que Pile et Face à chaque lancer (ne comptons pas les nombres de tranches :-) ) est donc 2²ⁿ.

Comptons le nombre de fois où le nombre de Piles est égale au nombre de Faces. Dans ce cas, on compte le nombre de façons de combiner les n Piles parmi les 2n lancers, c'est-à-dire , le nombre de combinaisons de n parmi 2n.
La probabilité d'obtenir le même nombre de Piles et de Face avec nos 2n lancers est donc le rapport des cas favorables sur le nombre de cas possibles soit :

Pour les habitués du monde des probabilités, on peut directement retrouver ce résultat en remarquant que le nombre de Piles suit une loi binômiale de paramètres p=1/2 (probabilité d'un Pile) et 2n pour la taille de l'échantillon.
On obtient alors que la probabilité d'obtenir autant de Piles que de Faces est la probabilité d'obtenir n Piles soit :

Jusque là, rien d'extraordinaire... mais regardez donc la formule de Wallis :

Ouais, on n'est pas très loin...
Remodelons un peu tout cela :


et comme n+1/2 ~ n à l'infini

Eh oui ! La probabilité que le nombre de Piles soit égal au nombre de Faces fait apparaitre Pi lorsque le nombre de lancers tend vers l'infini.
Cette forme rappelle d'ailleurs la distribution gaussienne, ce qui n'est pas très étonnant lorsque l'on sait que si p est fixé, la distribution binômiale tend vers la distribution gaussienne lorsque n tend vers l'infini (comme toute bonne loi qui se respecte, grâce au théorème central-limite !).
Plus précisément, pour notre loi avec X le nombre de Piles suivant une binômiale, on a où f est la densité de la loi de X-n. Dans le cas du passage à l'infini, la loi discrète binômiale devient une loi continue et l'on effectue alors ce que l'on appelle la correction de continuité c'est-à-dire que P(X=n) (ou P(X-n=0)) devient . On obtient donc comme approximation asymptotique de la probabilité d'obtenir autant de Piles que de Face :

Car l'exponentielle tend vers 1 lorsque n tend vers l'infini. On retrouve bien le résultat attendu en passant donc directement par l'approximation gaussienne. La cause est donc entendue, le Pi en proba, ce n'est que des histoires de proportions d'aires avec un cercle, ou bien cela provient de la constante de normalisation d'une distribution gaussienne !

Monte-Carlo

Non, je ne vais pas vous parler de Monaco, mais bien de la méthode d'approximation de Pi par la méthode de Monte-Carlo. En fait il y en a beaucoup, car le terme Monte-Carlo reflète une méthode d'approximation par tirage d'échantillons aléatoires. Cependant, une de ces méthodes est devenue très célèbre pour Pi, c'est celle du jeu de fléchettes.

Elle consiste à lancer (sans viser !) un nombre n de fléchettes dans une cible (de rayon 1/2) inscrite dans un carré et à compter la proportion de fléchettes arrivées dans le cercle par rapport au nombre total de fléchettes. Ce rapport tend vers la proportion de l'aire du cercle (Pi/4) sur celle du carré (1) c'est-à-dire Pi/4.

Formellement, on considère un carré de côté 1 et un cercle ionscrit dans le carré (donc de rayon 1/2).
Les fléchettes sont des réalisations d'une variable aléatoire de loi uniforme sur R². La distribution en est f(x,y)=1.

On considère la fonction g qui vaut 1 sur le cercle inscrit dans le carré et 0 sur le reste :

L'intégrale de cette fonction représente l'aire du cercle et comme celle du carré vaut 1, elle représente aussi le rapport de l'aire du cercle sur celle du carré. Et comme f(x,y)=1 on a :

Mais ceci n'est rien d'autre que l'espérance sous la loi uniforme de g(x,y). D'après la loi des grands nombres, on a donc la moyenne empirique qui tend vers cette espérance soit Pi/4 :

Il suffit donc d'après cette expression de tirer des couples de nombres aléatoires (x,y) (lancer des fléchettes !), de vérifier la proportion de ceux qui sont dans le cercle sur le total, elle tend vers Pi/4.
Bon, la convergence est éxécrable, mais c'est rarement l'intérêt des probabilités !
Ici, il est de constater encore que Pi apparait là où on ne l'attend pas (le jeu de fléchettes !) mais que ceci s'explique fort bien grâce à la présence du cercle (la cible).

---

B - Pi et les processus aléatoires

Pi n'apparaît pas seulement dans quelques théorèmes de probabilité isolés, il est aussi étroitement lié aux comportements du hasard ! si, si je vous assure... En témoignent par exemple les résultats obtenus sur les mouvements Browniens :
Définissons tout d'abord ce qu'est un mouvement Brownien, processus incourtounable de la théorie des probabilités !

1 - Quelques notions sur le Mouvement Brownien

Le mouvement Brownien ou processus de Wiener décrit un phénomène observé en 1827 par le botaniste écossais Robert Brown. Il observa que des grains de pollens en suspension dans l'eau suivaient un mouvement rapide et désordonné !
L'explication correcte du mouvement brownien est maintenant bien connue : un grain de pollen ou de poussière suspendu dans un fluide est soumis à un bombardement incessant par les molécules qui constituent le fluide. La quantité de mouvement d'une molécule isolée n'est jamais suffisamment importante pour que son effet sur la particule suspendue soit visible au microscope.

Cependant, si un plus grand nombre de molécules frappent en même temps la particule d'un côté, elles peuvent déplacer celle-ci de façon notable. L'union fait la force !

En 1905, Albert Einstein developpa cette théorie par une approche de type mécanique statistique. A partir de 1920, Nobert Wiener proposa une définition mathématique de ce phénomène, sous la forme d'un processus noté souvent W ou B :

• W₀=0
• pour tout 0st , W_t-W_s est une variable gaussienne N(0, t-s) (variance t-s) indépendante de la tribu engendrée par .

Comme W₀=0, on a W_t-W_s de même loi que W_t-s-W₀=W_t-s mais indépendant de celui-ci d'après la dernière propriété (les accroissements sont donc stationnaires en particulier). Celle-ci montre aussi une propriété tout à fait intéressante, celle qui montre que pour prédire le déplacement après l'instant s, la connaissance de la trajectoire avant l'instant s (la tribu engendrée ci-dessus) n'apporte aucune information de plus que la connaissance de la position à l'instant s.
Le mouvement Brownien est un fractal aléatoire dans le sens où son observation à n'importe quel zoom révèle toujours les mêmes discontinuités. Ceci est dû au fait que W_at et a^1/2W_t sont statistiquement indifférenciables (a fortiori de même loi), c'est une invariance d'échelle.
Le mouvement Brownien est continu mais pas dérivable à cause de l'expression de sa variance (divisez-donc W_t-W_s par t-s !)

Un des théorèmes importants de l'étude des mouvements Browniens, et qui justifie son existence mathématique, est le théorème de Donsker (mais je ne rentrerai pas trop dans les détails !) qui dit qu'une marche aléatoire converge en loi vers un mouvement Brownien au sens suivant :
Pour (Y_i) variables aléatoires indépendantes et identiquement distribuées sur l'espace probabilisé adapté telles que P(Y_i=1)=P(Y_i=-1)=0.5, et k dans {0,..,N}, , on définit :

En faisant se rejoindre les points k/N par des droites affines, on définit un processus X_t^N continu sur [0,1] (on pose X₀=0) qui converge en loi vers un mouvement Brownien lorsque N tend vers l'infini.
L'intégrale jusqu'à t d'un Bruit Blanc gaussien, classique en physique, est aussi un mouvement Brownien par exemple. C'est une manière simple de le construire :
On se donne un pas de discrétisation d>0 fixe et on pose t_n=d*n. On prend Z_i une suite i.i.d. de variables gaussiennes N(0,d) (variance d). Le mouvement Brownien standard unidimensionnel aux instants t_n est donné par :

en posant W₀=0.
Alors, vous me direz, quel rapport avec Pi, tout cela ?? C'est vrai, on ne voit apparaitre rien qui ressemble de près ou de loin à notre constante favorite ? Comment les fluctuations du hasard pourraient-elles connaître Pi ?
Et bien, c'est l'objet des quelques théorèmes limites en théorie des probabilités qui suivent. Faîtes gaffe, c'est de la haute voltige parfois !

2 - Les probabilités asymptotiques de petite boule brownienne

Soit un mouvement Brownien standard et la norme du sup.

2.a - L'équivalence de Chung (1948)

Ceci estime la probabilité que le mouvement Brownien dépasse une certaine valeur, lorsque celle-ci est très petite. C'est dingue de voir apparaitre Pi ici ! Ce théorème fondamental ouvre la voie à plusieurs variantes qui généralisent le résultat :

2.b - La probabilité de franchissement de Mogulskii (1979).

Si f₂-f₁>0 et Inf(f₂-f₁)>0 sur [0;1] alors

est bien sûr la mesure de Lebesgue sur [0;1].
Ceci donne la probabilité non plus pour une constante, mais pour des bornes variables sous forme de fonctions.
On est en plein dans les fluctuations du hasard, et celles-ci sont majorées par des bornes dépendant de Pi !


2.c - La probabilité de petite déviation de De Acosta (1983).

Soit g absolument continue sur [0;1] de dérivée de Lebesgue g' dans L₂([0;1],). Alors le 1.a se généralise en :

Bon, je ne vous dis pas que cela sert chaque jour mais c'est assez amusant de retrouver Pi dans cette galère, non ? En proba, Pi apparait fréquemment lorsque l'on a affaire à une loi gaussienne à cause de la constante de normalisation qui contient Pi. Mais comme on ne sait pas calculer la primitive de exp(-x²), il est souvent délicat d'isoler Pi. Eh ben ces théorèmes y arrivent et montrent que si le hasard parfait existait, ce qui semble tout de même le comble de l'incertitude, ce hasard dépendrait de Pi ! Très fort...

2.d - La probabilité de petite déviation de Berthet - Shi (2000).

Philippe Berthet est en passant notre bien aimé professeur de DEA de statistiques, autant vous dire qu'il assure, et que personnellement, je n'ai pas encore tout compris à son cours !

Si f0 vérifie soit (i) inf(f)>0 sur [0;1] soit (ii) f est croissante sur un voisinage V(0) de 0 alors

d'où l'on tire d'une part, que si f₂-f₁>0, si f₂-f₁ croissante sur V(0), si f₁+f₂ est absolument continue et si , alors le 1.b reste valable et donc lim₀f=0 est autorisé, et d'autre part, que l'on peut combiner le 1.c et le 1.d pour obtenir :

Mais que vient faire ce Pi au milieu, et dans une seule des équations ? Quelqu'un aura-t-il une explication métaphysique ? :-)

3 - Les lois limites presque sûres

La propriété d'invariance d'échelle permet de définir d'autres processus. Ainsi, soit W_T(.)=T^-1/2W(T.) une suite de mouvements browniens standards sur .[0;1] issus d'une trajectoire brownienne .

3.a - Loi du logarithme itéré de Chung (1948)

Ce résultat obtenu "presque sûrement" au sens de la théorie des probabilités (c'est à dire obtenu sur un ensemble de probabilité 1) nous montre par exemple que le mouvement Brownien considéré ne peut revenir infiniment souvent dans la boule uniforme centrée en 0, de rayon log(log(T))^-1/2.

Là-encore, on peut généraliser le résultat :

3.b - Loi de Chung fonctionnelle de Csàki (1980) puis de De Acosta (1983).

Soit qui est donc absolument continue sur [0;1] et telle que f(0)=0. Si alors

Lorsque =1, le problème est très délicat !. Csàki (1980), Grill (1991), Lifshits - Gorn (1999) puis Berthet - Lifshits (2001) trouvent la limite exacte (constante et vitesse) comme solution d'une équation entre , , et les variations de .

3.c - Module de non différentiabilité

Comme on l'a dit en présentant le mouvement Brownien ci-dessus, il n'est pas dérivable. Le module de continuité pour h n'admet pas de limite lorsqu'on le divise par h tendant vers 0, comme le montre le résultat suivant qui fixe donc un limite non pour h, mais pour . On n'atteint même pas complètement h^1/2, ce qui était prévisible intuitivement dans la mesure où, compte-tenu de la variance du mouvement Brownien, .

Le module exact de non-différentiabilité obtenu par Csörgö et Révész (1979) est le suivant :

Toujours cette fameuse constante limite comme dans la loi de Chung !

4 - Temps d'occupation de R⁺ par W sur [0;1]

Sans être totalement extraordinaire à cause notamment de l'arcsin qui ne fait apparaitre que comme une constante de normalisation, on peut encore citer le temps d'occupation de R^- par un mouvement Brownien

Les temps d'occupation d'ensembles par des processus sont souvent caractérisées par des distributions de type arcsin. Les premières du genre ont été étudiées par Lévy, notre grand probabiliste français.

---

Bibliographie

Voici quelques livres ou sites qui m'ont servi à la collecte des informations ci-dessus. Amusez-vous bien !

[1] Fabien Campillo, Frédéric Cérou, David Miglior, Simulation : de la loi uniforme aux équations différentielles stochastiques
http://www-sop.inria.fr/mefisto/java/tutorial1/tutorial1.html

[2] Yves Weiss, Université de Nice, Le mouvement Brownien
http://www.ac-nice.fr/physique/brownien/Brown.htm

[3] Sebastien Deguy, Université de Clermont-Ferrand, Tout ce que vous avez toujours voulu savoir sur le mouvement brownien fractionnaire, les processus gaussiens auto-similaires, l'intermittence, H, p et leurs estimations sans jamais oser le demander
http://llaic3.u-clermont1.fr/~deguy/publi/MBF/

[4] Monte-Carlo methodes in parallel computing
http://www.phy.hr/~laci/para/mc/mc.html#Integration

Enfin, merci à Philippe Berthet pour sa petite collecte de théorèmes de probabilités sur le mouvement Brownien !