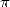|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Calculation of the decimals of Pi: Some new with old stuff!
To Sum up
By exploiting a simple geometric idea, Benoit, still as prolific, improves the efficients of Archimedes' method for the calculation of the decimals of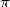 . This approach mixes algorithms and series and allows in
theory to obtain a convergence speed of as fast as we want it. The
convergence stays for the moment linear.
. This approach mixes algorithms and series and allows in
theory to obtain a convergence speed of as fast as we want it. The
convergence stays for the moment linear.
1 The Formula
A modern version of Achimedes algorithms
consiste of defining the algorithm
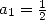 and
and
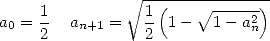 |
(1) |
which allows to calculate 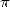 given that
given that
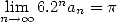 |
(2) |
The efficience of this method is not bad since
the convergence is in 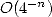 . It is not extraordinary either and numerous other
methods (algorithms, series...) also converges linearly, equlas it or
are an improvement (without taking into account the algorithms by
Salamin-Brent or the other Borwein's brother of course). We offer still
to start from this old idea and to calculate the decimals of
. It is not extraordinary either and numerous other
methods (algorithms, series...) also converges linearly, equlas it or
are an improvement (without taking into account the algorithms by
Salamin-Brent or the other Borwein's brother of course). We offer still
to start from this old idea and to calculate the decimals of 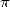 with a speed of how great we choose it to be (according
to a pre calculation). Hence, for all values of
with a speed of how great we choose it to be (according
to a pre calculation). Hence, for all values of 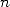 we have the following formula which stay valid:
we have the following formula which stay valid:
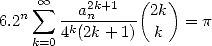 |
(3) |
2 Proof
We ask you to exactly calculate the strippy area below, which is a sector of a unit square.
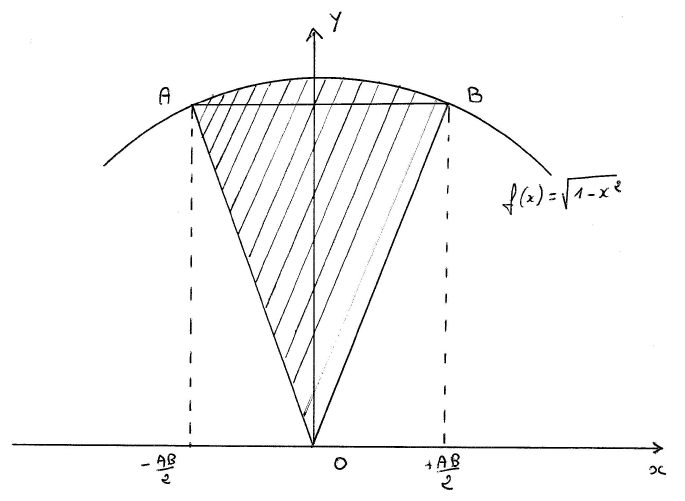
It is easy to see that this surface is worth
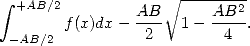 |
(4) |
By choosing 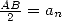 , we have for all
, we have for all 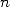 the cercle divided into equal sectors and :
the cercle divided into equal sectors and :
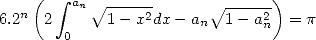 |
(5) |
because we find again the area of the unit circle. On the other hand, we have the well known series :
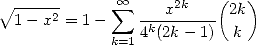 |
(6) |
i.e. 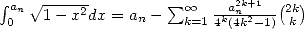 and
and 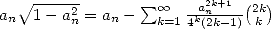 and hence
and hence 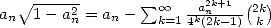 . The equation 5
hence becomes
. The equation 5
hence becomes
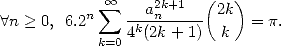 |
(7) |
This gives a family of series converging as
fast as we want towards 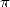 and hence improves Archimedes' algorithm .
and hence improves Archimedes' algorithm .
3 Trials
For 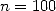 , if we calculate
, if we calculate 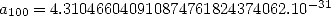 , then
the serie
, then
the serie
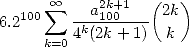 |
(8) |
gives however 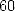 good decimals of
good decimals of 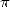 at each term.
at each term.
Other ideas by Benoît Cloitre
back to home page

 and
and  in a mirror
in a mirror and
and 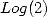 in a mirror
in a mirror