|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Benoit Cloitre
A Christmas formula for 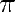
Benoit Cloitre offers a Christmas formula for 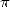 to us !
to us !
Formula
If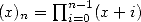 is Pocchammer's symbol, we obtain this general formula for
is Pocchammer's symbol, we obtain this general formula for 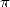 ,
true for any
,
true for any 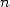 :
:
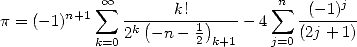
Proof
Let 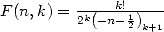 and
and 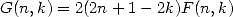 . It is easy to check the WZ-type relationship :
. It is easy to check the WZ-type relationship :
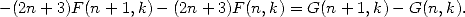
Thus, using notations in [Wilf], we obtain
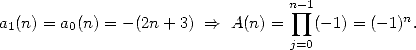
Moreover, 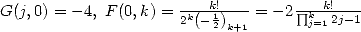 . The classical Euler's sum
. The classical Euler's sum 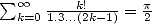 gives
gives 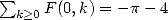 . Now, finally, from [Wilf], we obtain:
. Now, finally, from [Wilf], we obtain:
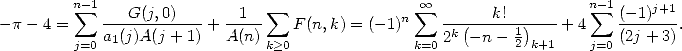
And so, 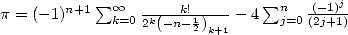 as wanted.
as wanted.
References
[Wilf] H.S. Wilf, Accelerated series for universal constants, by the WZ method, Discrete Mathematics and Theorical Computer Science 3, 1999, 189-192.
Home page
