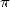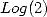|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Benoit Cloitre
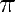 and
and 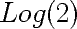 in a mirror
in a mirror
Benoit Cloitre, still very creative, is pursuing his chronicles about resemblance between famous constants, after those between  et
et 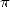 .
.
1 For 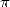
Let 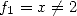 and
and 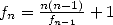 then
then 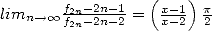 . Thus, if we write down
. Thus, if we write down
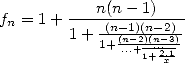
then we obtain an inverse Brounker-like continued fraction.
2 For 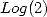
Let 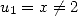 and
and 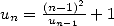 then
then 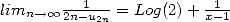 . The equivalent continued fraction is
. The equivalent continued fraction is
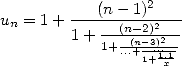
Proof for Pi
It is easy to see by induction that 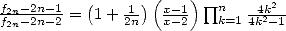 and we recognise the
Wallis product.
and we recognise the
Wallis product.
Proof for 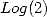
Let 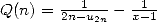 . We easily see that for
. We easily see that for 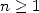 ,
,
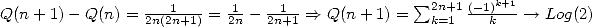 .
.
Checking under the software Pari-GP
For Pi
-
x=171679;u=x;for(n=2,100,u=n*(n-1)/u+1;if(n%2==0,print1((u-n-1)/(u-n)-prod(k=1,n/2,4*k^2/(4*k^2-1))*(1+1/n)*(x-1)/(x-2),",")))
,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
For log(2)
-
f(n)=if(n<2,171679,(n-1)^2/f(n-1)+1);Q(n)=1/(2*n-f(2*n))-1/(171679-1);for(n=1,10,print1(Q(n+1)-sum(k=1,2*n+1,(-1)^(k+1)/k),","))
0,0,0,0,0,0,0,0,0,0,
Home page