|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Benoit Cloitre
e and in a mirror
Benoit Cloitre is a brilliant maths amateur when he wants.
Consider the sequences ![]() n and
n and ![]() n to be defined as
n to be defined as
u1= 0, u2 = 1, un+2 = un+1 + 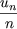 |
v1= 0, v2 = 1, vn+2 = 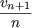 + vn + vn |
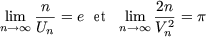
In general, for
u1=
x, u2 = y, un+2 = un+1 + 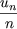 |
Then
lim n![]()
![]()
![]() = x +
= x + ![]()
By considering those two
sequences, e and  are mirrored! However, the speed of convergence are
very different... Un
converges very quickly (faster and faster) while
V n converges in a logarthmic way...
are mirrored! However, the speed of convergence are
very different... Un
converges very quickly (faster and faster) while
V n converges in a logarthmic way...
Benoit Cloitre first offered a direct prove, but one can prefer Gery Huvent's prove, from Lille, which allow us to find a general method to prove those sequences.
2.1 ForCalculating the first
few terms 0,1,1,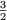 ,
,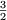 ,
,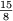 ,
,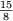 suggest that
suggest that
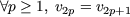
This property can be prove by induction on p, since it's true for p = 1. Suppose that v2p = v2p+1 then
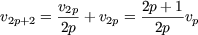
and
| v2p+3 | = 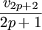 + v2p+1 = + v2p+1 = 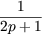 * * 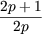 vp + v2p vp + v2p |
= 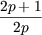 vp = v2p+2 vp = v2p+2 |
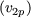 p
satisfy
p
satisfy
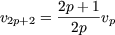
which by induction give us
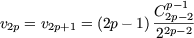
Taking into account the classical equivalence (obtain with Wallis)
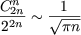
we have
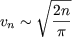
Note We can find a limited development with Stirling's formula, to get
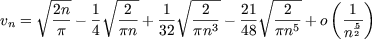
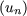 n
n
Consider the function
that generates the sequence 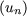 n
n
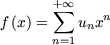
the given recurrent sequence can be written as
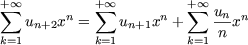
or
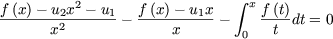
by differentiating, we get
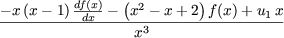 = 0
= 0
hence f is the solutiong to the differential equation
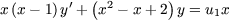
which has the general solution
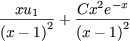
taking into acount than
u1 = 0 and u2 = 1 = 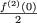 we find
we find
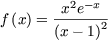
Now we need to determine the development of the power serie of f so to find each term of the sequence. For this note that
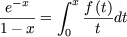
( 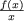 = v2x
+ v3x2 + ....is defined in 0 )
= v2x
+ v3x2 + ....is defined in 0 )
Then, we remember that if
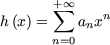
then
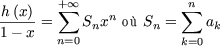
using Cauchy's product of two series. Hence
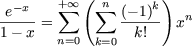
and
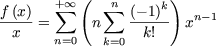
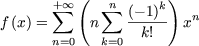
and
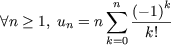
more particularly
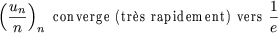
Note If we
did the same for the sequence
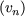 n, the generating
function is a solution to
n, the generating
function is a solution to
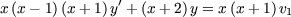
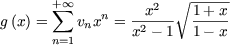
which satisfy
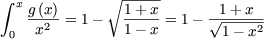
with
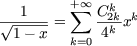
back to home page
