|
|
|
|
|

Benoit Cloitre
Une formule de Noël pour 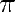
Benoit Cloitre nous offre une formule de Noël pour 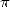 .
.
Formule
Si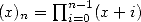 est le symbole de Pocchammer, nous obtenons cette formule générale pour
est le symbole de Pocchammer, nous obtenons cette formule générale pour 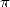 ,
valable pour tout
,
valable pour tout 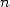 :
:
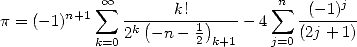
Preuve
Soit 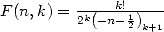 et
et 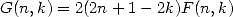 . Il est aisé de vérifier la relation (de type
WZ) :
. Il est aisé de vérifier la relation (de type
WZ) :
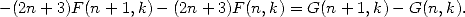
Puis, en utilisant les notations dans [Wilf], on obtient
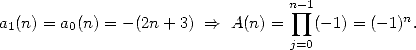
En outre, 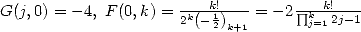 . La série d’Euler classique
. La série d’Euler classique 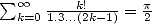 donne
donne 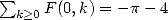 . Pour finir, d’après [Wilf], on obtient:
. Pour finir, d’après [Wilf], on obtient:
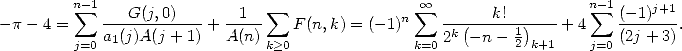
Et donc, 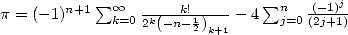 comme voulu.
comme voulu.
References
[Wilf] H.S. Wilf, Accelerated series for universal constants, by the WZ method, Discrete Mathematics and Theorical Computer Science 3, 1999, 189-192.
Retour à la page d'accueil
