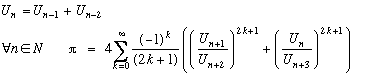Archimède : (287 AVJC - 212 AVJC)

Fibonacci : (1180 - 1250)

Geometrical application of the Fibonacci's suite :

U₀ and U₁ being strictly positive, (if equal to 1, it is the Fibonacci's suite !),

With the golden number,

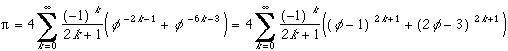
Al Kashi : (? - 1429)

De Cues : (1401 - 1464)

Viete : (1540 - 1603)

Descartes : (1596 - 1650)

Wallis : (1616 - 1703)

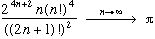
(the third one is just an improved version of the second one)

Other formulas : (see the Attic )

1)

2) Small formula on my own



3) Application of the law of large numbers


Let be a random sequence of n points in the square [0,1]x[0,1] and D_n the size of the set of these points in the circle of center 0 and radius 1, i.e. , then .

4) Isolated sequence