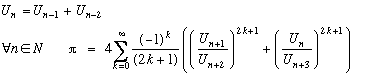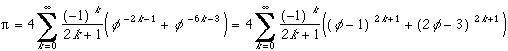Leonard of Pise - Fibonacci
(1180 - 1250)

U₀ and U₁ being strictly positive, (if equal to 1, it is the Fibonacci's suite !),

With the golden number,

Slice of life:

Fibonacci was born in Pise in 1180. Son of a toscan storekeeper (Bonaccio, from whichthe nickname), it is brought to travel much, notably in the middle East. Fascinated by the Arabic numbering that he discovers, he introduces it into the Westerner world by drawing up a work of explanation on his return (Liber abaci). This allows him to study more easily the equations of order 1 and 2 and, as it is seen in the historic of records, to calculate some decimal of Pi!
Fibonacci remained very famous thanks to its series and to the fact that he is almost the only Westerner mathematician of talent at this time.
The series was to resolve supposed problem according to:
*One considers a couple of rabbits which reproduces. How much we shall obtain from couples of rabbits after a number given of month knowing that every couple produces every month a new couple, which becomes productive only after two months (on 1202, according to mathematicians of A in Z, see Biblio)

About

Fibonacci never obviously wrote the previous result, but his series and its derivatives are in the heart of this formula, and he began a calculation of the decimal of Pi ( 3,1418 ); the interest for this constant deserved anyway a place on this site!

Proof

it is essentially geometrical...
Given a recurring series of the type: U_n=U_n-1+U_n-2
4 consecutive terms of this series are considered : U_n, U_n+1, U_n+2, U_n+3
Given 6 acute angles ß, ß', ß", µ, µ', µ" contents in the following figure, the rectangle of sides U_n+3=U_n+2+U_n+1 and U_n+2=U_n+1+U_n




One has according to the plan OM=ON because [OM] and [ON] is the hypotenuses right-angled triangle of base U_n+2 and height U_n+1.
The hatched triangles are the same by rotation of angle /2 so µ"=µ' now ß"+µ'=/2 so ß"+µ"=/2 and the triangle is isosceles rectangle in O (check, all right, it is not flagrant on the picture!)
The other internal angles of the triangle have so for measure /4 so µ-ß=/4 and ß'+µ'=/4
Now tan(ß)=U_n / U_n+3, tan(µ)=U_n+2/U_n+1
and tan(ß')=U_n / U_n+3, tan(µ')=U_n+1 / U_n+2

Where from /4=Arctan(U_n+2 / U_n+1)-Arctan(U_n / U_n+3)
and /4=Arctan(U_n+1/U_n+2)+Arctan(U_n/U_n+3)

Fibonacci's series being increasing, second equation is a sum of arctan numbers 1. By applying development limited of arctan in 0 (who is valid until 1) in the second of the previous two equalities, we obtain :


Even stronger!
Each knows that quotient U_n+1/U_n tends towards the golden section =. So it is easy to see that U_n/U_n+3 tends towards 1/³. In passing in the limit for n in the last sum, one has so :


After e and , here is that and are fervently linked !

Trials

We kwon very well the linear convergence of series of Arctan, let us give rather some of the equalities that one can obtain thanks to this formula :

/4=Arctan(U_n+1/U_n+2)+Arctan(U_n/U_n+3) below noted U_n+1/U_n+2+U_n/U_n+3 by simplicity !

n=0	1/2+1/3 (Formule Euler's formula)
n=1	2/3+1/5
n=2	3/5+1/4
n=3	5/8+3/13
n=4	8/13+5/21
n=5	13/21+4/17
n=6	21/34+13/55
n=10	144/233+89/377

One obtains a perfectly countable set of series converging towards ...