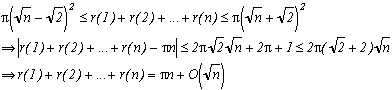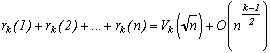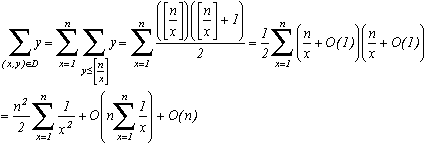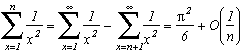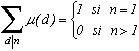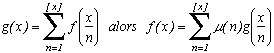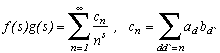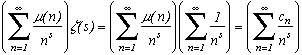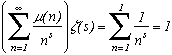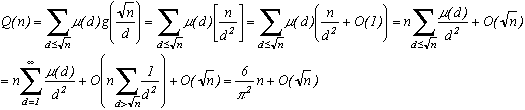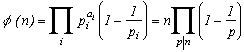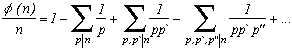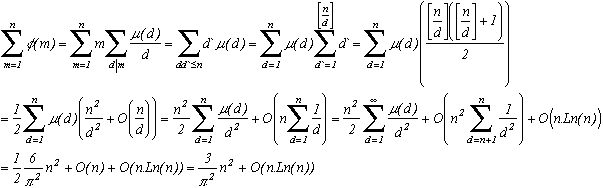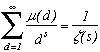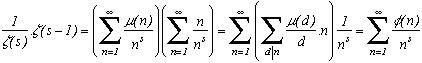Gauss (1777 - 1855) Möbius (1790 -1868) Euler (1707 - 1783)

Arithmetic Functions and Pi
Gauss' r(n) / Sum of Divisor / Möbius / Euler's Indicator

1) Gauss' function r(n)

    let r(n) be the number of way to decompose a natural number n into to squares,
    then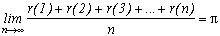

2) Function (n) sum of divisor

Let (n)= that is the sum of positives integers that divides n.
Then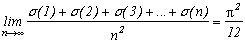

For more information on the fonction (n) of Möbius, cf.A000203

3) Möbius' function µ(n) 

Let µ(1)=1 ; µ(n)=0 if n has at least one squared factor >1
  and µ(p₁p₂...p_k)=(-1)^k if p₁, p₂, ..., p_k are distinct prime numbers.
(exemple µ(2)=µ(7)=-1, µ(4)=µ(8)=0, µ(6)=µ(10)=1)
Then for s>1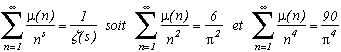
There exists many interesting results concerning this function. For example there's the following suprising formula  : by considering Q to be the set of nN* who don't have any squared factors, (i.e such that µ(n)=1) we obtain the rather nice following formula :

This approach allows us to state this magnificant theorem : The probability that an integer has no squared factors is

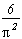
For more information on Möbius' function, cf.A008683

4) Euler's indicator function (n)

    Let (n) be the number of naturals stricly less than n and which are coprime with n (no common factors with n). For more information on Euler's function cf.A000010
    Then otherwise as and
This function allows us yet again to demonstrate quite nicely Cesàro's function.

A few word on Möbius

Our dear Möbius is a German mathematician born in 1790 in Saxony. He studied at Göttingen under the tutorial of Gauss and became an astronomer in Leipzig. Living for this science, he was nevertheless fascinated by maths. He had a special interest in projection geometry and number theory where he introduced his famous function.

More on

The arithmetic functions studies in the 18th and 19th Century often had simple definitions but their properties always seemed to appear out of nowhere. Who would have ever thought that some properties on the integers could ever link up with the world of the reals? Of course, you can't count on them to break records on decimal calculations, but suprisingly, a few present here within the most well know, have a very stong link with Pi !
Most of the time it's due to the value of Riemann's Zeta function, but do understand this, let's examine in more detail each function.

Demonstrations

1) Gauss' function r(n)

So, let's remind ourself that r(n) is the number of way to decompose n into 2 squares, combinations included. That is we also include in this number the trivail combinations with multiplication by -1 or the order of the squares.
For example, taking 5, we get :
5=(+/-1)²+(+/-2)²=(+/-2)²+(+/-1)²
therefore r(5)=4+4=8.
The properties of that function were mostly studied by Gauss and Jacobi.
The first demonstrated the result we want, and that has a nice geometrical explenation.

If we consider a disc of radius , that is which has equation x²+y²=, we can see that the integer couples (x,y) that satisfy x²+y²= where pn are within the disk as shown in the figure on the right (they are on the edge of the circle radius whuch is smaller that the one of radius , they are the dots inside the circle). Draw for each of thoses dots in the disk a square which the lower left corner is that point.
We then get a funny figure, which we'll call the domain D_n, where the area is the number of squares (of sides and so area 1) which it contains.
 But r(p) for pn counts the number of dots that are on the circle of radius hence all the dots inside the disc is counted in a r(p) for pn. Therefore, the number of points and associated squares is r(1)+r(2)+...+r(n).
The area of the domaine D_n shown above is therfore r(1)+r(2)+...+r(n).
But D_n is included in a circle of radius , that is the radius of the first circle + the diagonal of square 1 unit length (Look at the figure, the only thing of the domain that is not in the circle is never greater than the diagonal of a square, as marked)
Similarly, this domain can contain a circle of radius . Those disk have an area of so in the end we have sandwitch the area of D_n :

There we go !
We do get
Instead of considering O(), we could find for what minimal power of n (call it a) the result is still valid, in other terms, what is the speed of convergence.
As Autour du nombre Pi by Eymard/Lafon remind us, it's has been a reasearch issues for the last one and a half century.
 It has recently been found that a1/2. Hardy and Landeau proved seperatly that a1/4. The conjucture is that a=1/4 but it has yet to be proved. The best know coefficient for the moment is a22/73 and was found by Huxley (1993).

In the same style, we can generalise r_k(n) the number of decomposition of n as the sum of k squares. This comes down to work not in R² like we did for two squares, but in R^k.
We even get
  withV_k(R) being the volume of a sphere of radius R in dimension k.
But from the attic, we know this is equivelant to :

for dimension m.
Therefore we can conclude that :

with

---

2) Function (n) sums of dividors

Once again let's remind ourself that (n)=, that is the sum of positive integers that divide n.
A few example, just to make it clear !
(1)=1, (2)=1+2=3, (6)=1+2+3+6=12, (12)=1+2+3+4+6+12=28
This function is multiplicative for any to integers that are coprime.

Let's plunge in straight away in the deep end and do a bit of counting.
(1)+(2)+...+(n) contains the dividors of each naturals n counted a certain number of time, and we add them all up. We are going to find out this "certain number of time" for each divisor.
We start by fixing an x between 1 and n, first we look for the y_p such that xy_p=p, pn.
So for the set of pn, we then have counted the number of time each divisor y_p of (p) appear as well as the divisors of x. Then, we sum the y_p on all the x, and we will obtain the wanted value of (1)+(2)+...+(n).

Consider the line xy=n in the plane as shown on the right.

Fixing x is the same as counting the y such that xyD.



Thefore using the notation [a] to be the integer part of a, we get
(1)+(2)+...+(n)=

but we know that by taking the greatest value of each term so

We also know that gamma, Euler's constant is
so and finnaly

(1)+(2)+...+(n)=n²+O(n.Ln(n))

Great, two down and two more to go....
As with 1), intense research are still being done on the best possible remainder, and for the moment A. Walfisz has the prize with O(n.Ln^2/3(n)) found in 1963.

---

3) Möbius's function µ(n)

  Let µ(1)=1 ; µ(n)=0 if n contains at least one squared factor>1 and µ(p₁p₂...p_k)=(-1)^k if p₁, p₂, ..., p_k are distinct prime numbers (exemple µ(2)=µ(7)=-1, µ(4)=µ(8)=0, µ(6)=µ(10)=1).
Lemmae
1) One of the first (quite amazing) property of this function is the following:

Proving this is fairly simple, the result is obvious by definition for n=1. Taking now an un n>1 and show that the sum is nul.
The integer n is as always the product of prime factors hence we can write it :
n=p₁^a1p₂^a2...p_k^ak. If we want to find the sum of the divisor of n, this is the same as taking the sum of the primes p_i, then the couples of primes p_ip_j , then the triplets, etc.. therefore :

using the definition µ(p₁p₂...p_k)=(-1)^k and then we count the number of couples, triplest that can exists in the sum (hence the combinations) and finnaly, we can see Newton's binomial formula.

2) µ is a multiplicative function, and provide a strong results that make it possible to inverse certain formulae :

(We do get )
  Demonstration:
Ok, so this is all good, but now for the demonstration that we want :

Proving that :

We will need a small lemma, that we'll call Dirichlet's Lemma :
Let f(s) and g(s) the series said to be Dirichlet to be defined as :
. Multiplying those two series gives us:

Now using this Dirichlet multiplication we can calculate:

with so finnaly

whith the result

---

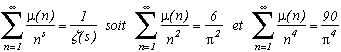
This is not all, if we go further, as mentioned above, by considering Q the set of intergers nN* who don't have any square factors in it's decomposition (that is such that µ(n)=1) we obtain the lovely following formula:

The prove in itself is not very difficult but it needs a rather long generalistion of certain results, and for the moment, I don't want this page to turn into a monster... Though I can't resist the pleasure of being able to show a small result which I find even more impressive:

The probability that an integer is without any squared factors is

Prove :

Define Q(x) for real x the number of integers k less than x and who don't have squared factors. Using the definition of Möbius' function, we can write for n integers :
Q(n)=. To prove the theorem, we just need to look at the proportion of Q(n) compared to n, that is to show that

Q(n)=n+O(n^1/2)

The basis of it consit first of all to place an integer k whose biggest squared factor is d² in a set E_d. We do this for all kn. For E₁, obviously, correspond to the set of integers without squared factors. And since there are no squared factors greater than n^1/2 in n (Again obviously!), E_d is empty for d>n^1/2. Counting the numberf of element of E_d:
It is fairly evident that card(E₁)=Q(n).
For the others E_d, take k=d²*k' in E_d.
k'n/d² since kn.
  Furthermore, k' does not have any squared factors because if it had one (call it a for example), a.d will also be a squared factor of k and since a.d>d, k would belong to another E_i. So in the end card(E_d)=number of k'n/d² without any squared factors, hence : card(E_d)=Q(n/d²)

Since we have n non nul integers less than n (!), and that they are all included in a E_d, we can write :

Following this, if we aplly the famous inversion formula of Möbius to f(x)=Q(x²) with n^1/2=x
  and so to g(n)=n², g(x)=[x²] for real x.

This formula allows the following calculation, with (it seems to me....) quite obvious steps :


Finnally, for O(sum), the result comes from :

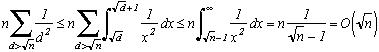
4)   Euler's Indicator function (n)

    Recall : (n) the number of integers strictly less than n and that are coprime with n (don't have any common factors with n).

  Lemmae:
1) A first lemma states that is multiplicative for two integers m and n that are coprime, i.e.

(n.m)=(n).(m)

It is true, if we try to evaluate (n), we start from the definition : according to Bézout's theorem, k and n are coprime if and only if there exists integers u and v such that u.k+v.n=1 so this is equivalent to k inversible modulo n.
Therefor (n) is the cardinal of the inversibles groups of Z/nZ. Since m and n are coprime, according to the famous chinesse lemma, there exists an isomorphism between Z/mnZ and Z/nZ*Z/mZ so the  inversibles groups of those two rings have the same cardinality and (n.m)=(n).(m).
(phew, this brings back some painful memories of algebra!)

2) Now, if we want to evaluate for all n, let's start by decompose this poor integer: n=p₁^a1p₂^a2...p_k^ak , a_i being an non nul integer, and calculate for p_i^ai :
Between 1 and p_i^ai (not included), there's p_i^ai-1 integers (!) and since the only multiples of p_i are factors of p_i^ai as p_i prime, those factors are :
pi, 2pi, 3pi, ..., (p_i^ai-1)p. So there are p_i^ai-1.
So the number of integers that are coprime with n is :

(p_i^ai)=p_i^ai-1-number of divisors of n=p_i^ai-1-(p_i^ai-1-1)=p_i^ai(1-1/p)

And since the p_i^ai are evidently coprime between them, we can work out (n) thanks to the multiplicity of :

For example, 500=2²5³ so (500)=500(1-1/2)(1-1/5)=200.

3) Developing the following product, we get :

If we have d=p₁p₂...p_k, the p_i being all disctint like in the sum, then µ(d)=(-1)^k so .
Therefore, in all cases, we can write :

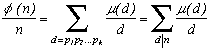
  because if d has a prime factor squared, the Möbius' function applied to d is nul by definition.
Cool...

  Prove:
Ok, now we need to show that then ...

We suspected for quite a while, that the previous lemma using Möbius' function was going to be very useful!
Let's plunge straight in the calculation :


Phew...
Here again, numerous research end it up with a new masterpiece by Walfisz (1963) who found the best remainder known today, O(n(Ln(n))^2/3(Ln(Ln(n)))^4/3).

To prove the second fomula, we are going to use Dirichlet's multiplication and the result demonstrated above:

  There we go! It wasn't that hard, was it ? But we just simply need to dive in...

This last formula allow us for example to find :

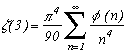
One last consequence of this result is the famous theorem of Cesàro ! It's unbelievable to find it here, but the definition of Euler's Indicator function was hinting at it. Truly, count the number of integers couple (p,q) included between 1 and n. If p=1, q can take the value 1 to n, hence n values. If p=2, q can take the value 2 to n (since (2,1) was already counted previously under the form (1,2) when p=1) hence n-1 value, and so on until p=n. So there are 1+2+3+...+n=n(n+1)/2 couples (p,q).
The number of integers coprime with fixed p is simply the value of the function(p) by definition. So up to n, the number of integers couple (p,q) that are coprime is (1)+(2)+(3)+...+(n).
So the probability that two positive integers are coprime is equal to the limit of the sum proportion of the (k) (favorables cases) on the number n(n+1)/2 of coup;es (p,q) (total cases) i.e. :

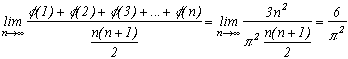
Great!.....

Trials

Puff, no need! The arithmetics function are not at all made for that and anyway depend for most of them on the serie (s) so also experience a sad logarithmitic convergence....