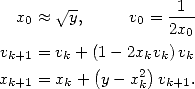|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Newton’s method
1 The roots of the problem
Let’s imagine that you’re asked for the first digits of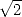 . Silence for a few seconds... mmmh... well, it’s
above 1, less than 2 because
. Silence for a few seconds... mmmh... well, it’s
above 1, less than 2 because 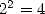 ... It’s less than 1.5 since
... It’s less than 1.5 since 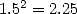 etc... Nothing very simple... So
how could the mathematicians of the 17th century numerically compute the roots of a 4th degree polynomial
?
etc... Nothing very simple... So
how could the mathematicians of the 17th century numerically compute the roots of a 4th degree polynomial
?
Always prolific, Newton proposed around 1669 (!) an iterative algorithm converging quadratically towards roots of a number. Quadratically means that the number of correct digits of the numerical estimate doubles at each step. Thenceforth, algorithm complexity of the division and roots extraction becomes equal to that of multiplication. A godsend for modern computations, where bruising roots extractions are experienced in the algorithms of Salamin or those from the Borwein brothers. The Newton’s algorithm a several qualities, which are exposed in the following paragraphs.
2 Wording of Newton’s method
Originally, i.e. more than three centuries ago, Newton’s method was used to numerically estimate a root  in
the equation
in
the equation 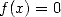 . Actually, this algorithm allows to show the complexity equivalence of multiplication,
division and roots extraction.
. Actually, this algorithm allows to show the complexity equivalence of multiplication,
division and roots extraction.
In 1669, Newton proposed an iterative algorithm to find roots of polynomial (Newton’s iteration). Then, Raphson reworded it in a more modern way in 1690. Simpson, Mourraille, Cauchy and Kantorovich completed it and made it more general, which finally gives the following wording:
Theorem 2.1 Let 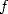 be analytic in a complex neighboring of
be analytic in a complex neighboring of  . Let’s suppose that
. Let’s suppose that 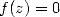 and
and
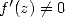 . Then, the following algorithm
. Then, the following algorithm
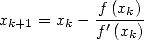 | (1) |
uniformly and quadratically converges towards  when the initial value
when the initial value 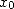 is chosen to be in a neighboring
of
is chosen to be in a neighboring
of  .
.
This algorithm has an amazing property of errors autocompensation : if 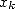 is modified such
that only
is modified such
that only 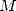 correct digits are left compared to
correct digits are left compared to  then
then 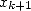 will have
will have 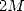 correct digits
though, given that enough digits are used at this step. In other words, the quadratic convergence is
preserved.
correct digits
though, given that enough digits are used at this step. In other words, the quadratic convergence is
preserved.
One straightforward consequence is that the computation of  to
to 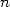 digits only require to
initialize the algorithm with a couple of correct digits, then double the number of digits taken into
account at each step until at least
digits only require to
initialize the algorithm with a couple of correct digits, then double the number of digits taken into
account at each step until at least 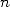 digits are reached. This dramatically reduces the complexity
of the computation and allows to show that multiplication, division and roots extraction are
equivalent.
digits are reached. This dramatically reduces the complexity
of the computation and allows to show that multiplication, division and roots extraction are
equivalent.
3 Applications
3.1 Multiplicative inverse of a number
Let’s choose a number 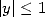 . We want to compute its multiplicative inverse with
. We want to compute its multiplicative inverse with 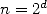 correct digits.
Using the function
correct digits.
Using the function 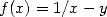 , the Newton’s algorithm becomes
, the Newton’s algorithm becomes
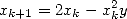 | (2) |
which is only using multiplications and additions. The equation
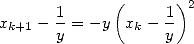 | (3) |
illustrates the quadratic convergence of the algorithm. Suppose now that we initialize the algorithm with one correct digit. We then have
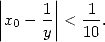 | (4) |
From the errors autocompensation property of the Newton’s method, we are allowed to only use
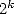 digits at the
digits at the 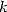 th step. And from 2, we only need
th step. And from 2, we only need  multiplications (
multiplications (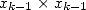 et
et
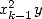 ) and
) and  additions (
additions (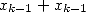 et
et 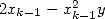 ) to obtain
) to obtain 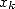 . Thanks to the
quadratic convergence, only
. Thanks to the
quadratic convergence, only 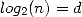 itérations of 2 are needed to obtain
itérations of 2 are needed to obtain 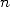 correct digits
of
correct digits
of 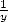 . If we define
. If we define 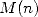 as being the complexity of a multiplication method applied to
as being the complexity of a multiplication method applied to 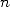 digits, given that the complexity of an addition will be
digits, given that the complexity of an addition will be 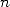 , we then obtain a final complexity
of
, we then obtain a final complexity
of
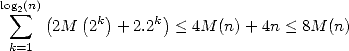 | (5) |
for the multiplicative inverse computation. Indded, we can reasonably suppose that 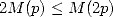 ,
which means that the complexity of
,
which means that the complexity of  multiplications of numbers with
multiplications of numbers with 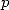 digits is slightly
less complex than the multiplication of two numbers with
digits is slightly
less complex than the multiplication of two numbers with 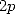 digits. From this ensues that
digits. From this ensues that
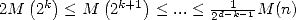 in 5. Thus, the multiplicative inverse is not far more
complex than multiplication (it’s a
in 5. Thus, the multiplicative inverse is not far more
complex than multiplication (it’s a 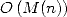 ). Moreover, since
). Moreover, since 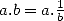 , division also is a
, division also is a
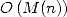 .
.
3.2 Square root extraction
Things also are going well. We can use the function 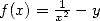 which leads to the estimation of
which leads to the estimation of 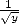 then we use the fact that
then we use the fact that 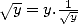 . The associated iteration is
. The associated iteration is
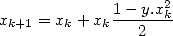 | (6) |
which practically leads to a final complexity of around 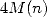 .
.
A natural alternative uses directly 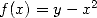 , but this leads to an iteration showing a
division:
, but this leads to an iteration showing a
division:
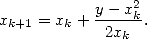 | (7) |
However, the prolific Schönhage, full of ideas (see also FFT), proposed to replace 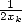 with another iteration
in 1971. He then obtained the following coupled iteration
with another iteration
in 1971. He then obtained the following coupled iteration
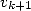 estimates
estimates 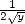 . this algorithm is called “Newton’s coupled iteration” ([5], p257) and practically
gives a complexity of around
. this algorithm is called “Newton’s coupled iteration” ([5], p257) and practically
gives a complexity of around 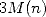 .
.
You can find several refinements of Newton’s method in [1, 4]. The complexity equivalence of multiplication, division and roots extraction is exposed in [2, 3].
References
[1] J. Arndt, C. Haenel, ” Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
[2] R. Brent, “Fast multiple-precision evaluation of elementary fonctions”, Journal of the Association of Computing Machinery, 1976, pp.242-251.
[3] S. A. Cook, S. O. Aanderaa, “On the minimum computation of functions”, Trans. AMS, 1969, vol. 142, pp291-314.
[4] M. D. Householder, “The Numerical Treatment of a Single Nonlinear Equation”, 1970, MacGraw-Hill, New-York.
[5] A. Schönhage, V. Strassen, “Schennelle Multiplikation grosser Zahlen”, Computing, 1971, vol. 7, pp. 281-292.
back to home page