|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
Modern era
Superfast algorithms based on the theory of modular equations and the arithmetico-geometric mean
(XXth century)
1976 :
a derived algorithm
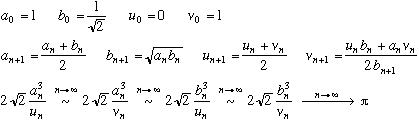
I haven't tested the following algorithms yet
Quadratic convergence
Cubic convergence
This sequence converges towards the multiple of Pi closest to f0.
fn=fn-1+sin(fn-1)
1) 1984 : quadratic convergence (based on the arithmetico-geometric mean)
2) 1987 : quadratic convergence (also based on the AGM)
3) quadratic convergence (based on modular equations as the following equations)
4) quadratic convergence :
5) cubic convergence :
6) quartic convergence :
7) quintic convergence:
8) septic convergence :
9) nonic convergence :
10) "hexadecimalic" (!) convergence (order 16)
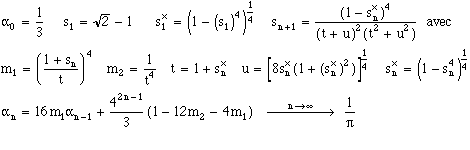
back to home page
