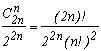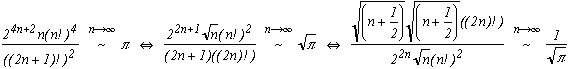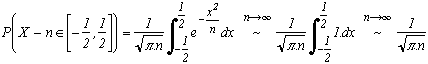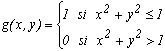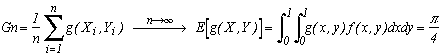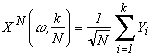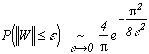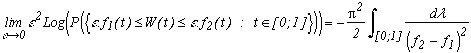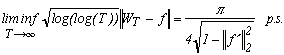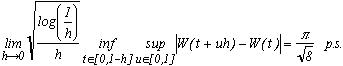Pi in random phenomena

This page is part of three pages dealing with the complex relations between Pi and the randomness field. This is indeed not easy to explain everything in one page ! I hope this page will grow as I will collect some new stuff. I'm open minded to any suggestion, of course. And I did not find all the proofs of what I present in the following paragraphs, so if you know one of them, please contact me !

This page is quite recent so it's less messy now than before. You are allowed to have a summary ;-)

A - Pi and the theorems related to probabilities

1 - Cesàro
2 - Buffon
3 - Coin tossing game
4 - Monte-Carlo

B - Pi and random processes

1 - Some notions about the Brownian Motion
2 - Asymptotic probabilities for small Brownian balls
3 - Almost sure limit laws
4 - Occupation time of R⁺ by W on [0;1]

and a couple of elements of Bibliography

---

A - Pi and the theorems related to probabilities

Pi appears in several isolated theorems often considered as belonging to the probability field. I would call these theorems some "lotto probabilities" (!) since it deals more with proportions, counts and areas estimations most of the time, than real probability theormes stemming from inherent measure theory !

However, some results are somewhat facinating and show Pi in domains where we wouldn't expect it (him !) to appear. The most famous theorems probably are Cesàro and Buffon ones, that we remind here (as the regular visitors already know where to find them on my website ;-)).

Cesàro's theorem

The probability of two randomly selected integers being coprime is ...
If we want to use this result, we have to reword the following sentence as the set of natural integers couples is infinite: if we choose two natural integers less than n, the probability P_n of them being coprime tends towards when n tends towards infinity.

A proof is available on the Cesàro's page.

Theorem of the Buffon's needle

Suppose we have a floor made of parallel strips of wood, each the same width 2b, and we drop a needle of length 2a onto the floor. The probability that the needle will lie across a line between two strips is




A proof is available on the Buffon's page.

Coin tossing game

Let's drop 2n times a coin, you probably have one somewhere in your pocket, haven't you ? The number of possible results is 2²ⁿ, since there is only head or tail (we will trust the coin to not fall onto the edge ;-)).

Let's count the number of times when we have equal number of heads and tails. In this case, we count the number of ways to combine the n heads among the 2n drops, that is , the number of combinations of n among 2n.
Thus, the probability to have the same number of heads and tails with our 2n drops is the number of favorable cases over the number of possible cases:

For the people accustomed with probability world, we can find this result by noticing that the number of heads follows a binomial law of parameters p=1/2 (probability of a head) and 2n for the sample size.
We then realize that the probability of having an equal number of heads and tails is the probability to have n heads:

That's straightforward ! Until now, nothing extraordinary... but have a look on the Wallis' formula:

Well, we're not so far...
Let's model the previous equation :


and as n+1/2 ~ n asymptotically

Yesss ! The probability to have an equal number of heads and tails make appear Pi when the drops number tends towards infinity.

By the way, the right member reminds us of the gaussian distribution, which is not so surprising insofar as when p is fixed, the binomial distribution converges towards the gaussian distribution when n goes to infinity (as every kind regular law, thanks to the limit central theorem !).
More precisely, with X the number of heads following a binomial distribution, we have where f is the likelihood of the distribution of X-n. Asymptotically, the discrete binomial distribution becomes a continuous distribution. We therefore apply what we call the correction for continuity: P(X=n) (orP(X-n=0)) becomes . We then obtain an asymptotic approximation of the probability to have an equal number of heads and tails :

because the exponential tends towards 1 when n goes to infinity. We eventually find the expected result using directly the gaussian approximation. So you will tell me "Why the hell does this constant appear in the integral of an exponential ?". I know, I know, that's the beauty of the beast...

Monte-Carlo

No, I don't want to talk about Monaco but about an approximation of Pi obtained by the so-called Monte-Carlo method. Actually, there are plenty of such methods, because the nickname Monte-Carlo describes a general method of approximation by picking up random samples. However, one of these methods has become very famous for Pi, that is the darts game.

Suppose we throw (without aiming !) n darts in a round target (of radius 1/2) inscribed in a square. We then count the proportion of darts in the circle over the total number of darts. This ratio tends towards the ratio of the area of the circle (Pi/4) over the area of the square (1) , that is Pi/4.

Mathematically, with the above hypothesis (circle of radius 1/2, square of side 1), the darts are observations of a random variable of uniform distribution on R². The distribution of this variable is therefore f(x,y)=1.

Let's consider the function g equal to 1 on the inscribed circle in the square and 0 outside :

The integral of this function represents the area of the circle. Since teh area of the square is 1, it also is equal to the ratio of the circle area over the area of the square. Since f(x,y)=1 we have:

The right member is nothing else than the expected value of the g(x,y) under the uniform distribution. From the law of large numbers, the empirical mean tends towards this expectaed value of Pi/4 :

From this expression, we just have to pick some couples of random numbers (x,y) (coordinates of the darts !), and check the proportion of those which are in the circle over the total. This ratio tends towards Pi/4.
Ok, I have to admit that the convergence speed is awful, but it is rarely the first interest of probabilities !
Here, one interest is to notice that pi appears where we don't expect it to appear (the darts game !) but this is well explained by the presence of the circle (the target).

---

B - Pi and random processes

Pi does not only appear in some isolated probability theorems. It also is closely related to the behaviour of randomness ! yes, I assure you it's true... For instance, let's talk about some results related to Brownian motions:

At first, here is a definition of a Brownian motion, unavoidable process of the probability theory !

1 - Some notions about the Brownian Motion

The Brownian Motion, or Wiener process, describes a phenomenon oberved in 1827 by the scottish botanist Robert Brown. He observed than pollen grains in water follow a jittery motion ! The correct explanation for this phenomenon is now well known: a pollen grain or a speck of dust floating in a fluid is permanently hit by molecules of the fluid. The force generated by an isolated molecule is not enough for the effect to be visible. However, if a larger number of molecules hit the grain simultaneously, the grain may noticeably move. Union if power !

In 1905, Albert Einstein developped this theory by the means of a statistical mechanical approach. After 1920, Nobert Wienerproposed a mathematical definition of this phenomenon, using a process usually calledW or B :

• W₀=0
• for any 0st , W_t-W_s is a gaussian variableN(0, t-s) (variance t-s) inindependant of the tribe generated by .

Since W₀=0, W_t-W_s has the same distribution than W_t-s-W₀=W_t-s but is independant of this latter because of the definition (the differences are stationnary in particular). Another interesting property stemming from the definition is that the prediction of the motion after the time s is not better with the knowledge of the trajectory before the time s (the generated tribe) than with the only knowledge of the position at the time s.
The Brownian motion is a fractal insofar as we'll observe the same discontinuities whetever the zoom we use to observe it. This is due to the fact thatW_at and a^1/2W_t are statistically similar (same distribution), that is a scale invariance.
The Brownian Motion is continuous but not differentiable because of the expression of the variance (try to divide W_t-W_s by t-s !)

One of the most important theorems related to the Brownian motion, and a rationale for its mathematical existence, is the Donsker's theorem: I won't be exhaustive on the subject, but this theorem roughly says that a random walk converges in law towards a Brownian motion as follows :
For some independant random variables (Y_i) having the same distribution on the probabilized space and such that P(Y_i=1)=P(Y_i=-1)=0.5, with k in {0,..,N}, , we define:

If we join the points k/N with lines, we define a process X_t^N continuous on [0,1] (we fix X₀=0) which converges in law towards a Brownian motion when N goes to infinity.
The integral of a gaussian white noise from 0 to t , a classic from physics, also is a Brownian motion for instance. This is an easy way to build one :
we fix a step d>0 and we define t_n=d*n. Then, let Z_i be an independant and identically distributed sequence of gaussian variablesN(0,d) (variance d). The standard unidimensional Brownian motion at the time t_n is given by :

given that we also fixW₀=0.
Then, you tell me, what is the link with Pi ? It's true that it is not obvious at first what looks like our favorite constant Pi. How the random fluctuations may know Pi ?? Yet, the following paragraphs deal with some limit probability theorems related to Pi. But be careful, they might scare some kids...

2 - Asymptotic probabilities for small Brownian balls

Let be a standard Brownian motion and let be the maximal norm.

2.a - The Chung equivalence (1948)

This expression estimates the probability of a Brownian motion being smaller that a given value, when this value is very small. It is crazy to see Pi here ! This important theorem gives rise to derived formula which generalize the result :

2.b - Crossing probability of de Mogulskii (1979).

If f₂-f₁>0 and Inf(f₂-f₁)>0 on [0;1] then

is of course the Lebesgue's measure on [0;1].
The Chung's equivalence is now given for variable bounds as functions.
We are completely into random fluctuations, and these ones are bounded by something related to Pi !


2.c - The small deviatio probability of De Acosta (1983).

Let g be absoltely continuous on [0;1], having g' as a derivative in L₂([0;1],). Then, 1.a can be generalized as follows :

Ok, I'm not telling you it's daily useful, but that is funny to find Pi in this mess, isn't it ? In probabilities, Pi often appears when a gaussian law is involved because of the normalization constant. But since we don't know how to compute the indefinite integral of exp(-x²), it often is delicate to isolate Pi. Well, these theorems do it and show that the full randomness depends oon Pi. Striking !

2.d - The probability of small deviation of Berthet Berthet - Shi (2000).

By the way, Philippe Berthet is our lovely professor in master of statistics. Believe me, he's strong and, personally, I did not understand everything in his course !

If f0 follows either (i) inf(f)>0 on [0;1] or (ii) f is growing on a neighboring V(0) of 0 then

from which it ensues that if f₂-f₁>0, if f₂-f₁ grows on V(0), if f₁+f₂ is absolutely continuous and if , then 1.b remains true and so lim₀f=0 is allowed. Also in this case, we can combine 1.c and 1.d to obtain:

Well, where does the Pi comes from and what is its role in all this mess ? Has anyone a metaphysic explanation ? :-)

3 - Almost sure limit laws

The scale invariance property allows to define other process. For instance, let W_T(.)=T^-1/2W(T.) be a sequence of standard Brownian motions on sur "."[0;1] coming from a Brownian trajectory.

3.a - Chung's Law of the Iterated Logarithm (1948)

This almost sure result (i.e. obtained on an set of probability 1) shows for instance that the Brownian motion can't come back indefinitely often in the uniform ball centered in 0, and having a radius log(log(T))^-1/2.

Here, again, we can generalize the result :

3.b - Functional Chung's law of Csàki (1980) and De Acosta (1983).

Let's define which is so absolutely continuous on [0;1] and such that f(0)=0. If then

When =1, the problem becomes incredibly intricate !. Csàki (1980), Grill (1991), Lifshits - Gorn (1999) then Berthet - Lifshits (2001) find the exact limit (constant and speed) as a function solving an equation between , , and the variations of .

3.c - Modulus of non-differentiability

AS we said before, the Brownian motion is not differentiable. The modulus of continuity for h has no limit when it is divided by h tending towards 0. The following result gives a limit for . We don't even reach h^1/2, which is logical insofar as, given the variance of the Brownian motion, .

The exact modulus of non-differentiability obtained by Csörgö and Révész (1979) is the following:

Still this staggering constant as a limit like in Chung's law !

4 - Occupation time of R^- by W on [0;1]

The follwing result is not absolutely fabulous because of the presence of the arcsin which make appear as a normalization constant. However, it is fairly beautiful. The occupation time of R^- by a Brownian motion is given by

The occupation time of sets by process often are characterized by arcsin-like distributions. First of these distributions were studied by Lévy, our great French probabilist.

---

Bibliography

Here are some books where I collected information about the previous theorems. Have fun !

[1] Fabien Campillo, Frédéric Cérou, David Miglior, Simulation : de la loi uniforme aux équations différentielles stochastiques
http://www-sop.inria.fr/mefisto/java/tutorial1/tutorial1.html

[2] Yves Weiss, Université de Nice, Le mouvement Brownien
http://www.ac-nice.fr/physique/brownien/Brown.htm

[3] Sebastien Deguy, Université de Clermont-Ferrand, Tout ce que vous avez toujours voulu savoir sur le mouvement brownien fractionnaire, les processus gaussiens auto-similaires, l'intermittence, H, p et leurs estimations sans jamais oser le demander
http://llaic3.u-clermont1.fr/~deguy/publi/MBF/

[4] Monte-Carlo methodes in parallel computing
http://www.phy.hr/~laci/para/mc/mc.html#Integration

Last but not least, thanks to Philippe Berthet for having collected some of the previous theorems !