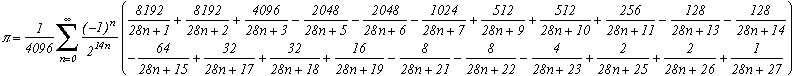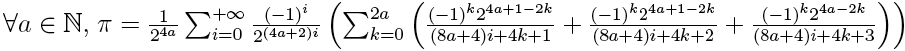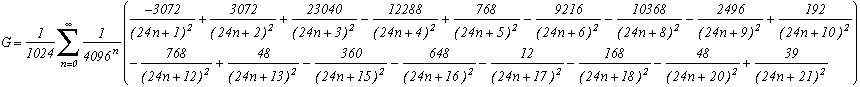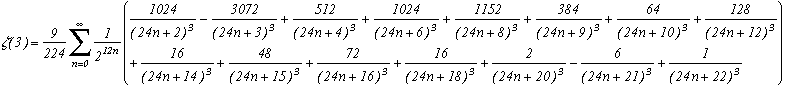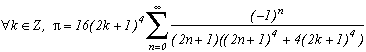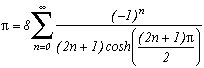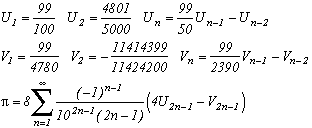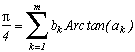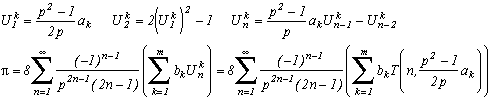A few personal ideas of formulas

 PDF version
 

Since I am interested in Pi, I  often entertained the hope of discovering a new mathematical property about this number, or about an other one, which wouldn't have been discovered. Obviously, my name is not Euler and at my level,  as statistics student, it's quite difficult to be efficient. Mathematics remain for me a dream.
Nevertheless, I have sometimes few ideas which I don't know what it is worth, but it don't stop me to try to use it! Several net surfers have directed me towards interesting domains which permit, after some collaborations more than fruitful and very enlightening for me, to get back of it some nice formulas.
Witness, the following expressions, I don't know if they are known, I don't think moreover for some of them ! If you are interested a bit in underlying mathematics you will, I hope so, lead to appreciate them, to criticise them (!), to say me if you have other ideas, etc...
At last now we're getting there, I talked enough, I let you discover those modest contributions...

NEW BBP formulas very fast for various constants

Pi=



and more generally


This formula has not been demonstrated yet.
(I will put some others here soon, I have a cargo of it, but I have to put them in the correct manner !)

Catalan's constant=G



This formula is now demonstrated. The proof will be available soon.

Zêta(3)=(3)



(This one is my favourite, because as far as I know, after having looked for, we absolutely didn't know BBP  formulas to calculate Zeta(3) (when I found it, 2000), and it makes it possible in addition a fast calculation of decimals!)

The demonstration of the previous formula is explained in the following file in pdf/ps format (It is a polylogarithm matter a bit complicated...) :
pdf format
ps format

Various other contributions

They are already present on the web site but you might have not seen them !

1) There is obviously the formula of my youth :

which I learnt that it was known in the early 90's, what didn't strike me given its simplicity ! But I like it in particular because she is dated from the time when my friend David and my self (I was 16 and I only got the baccalaureate) have decided after its discovery to do the synthesis of the series which converge on Pi. That's how it has begun !!
(it is built by considering a circle where you fit vertical trapezium into. By calculating the area of those trapezium in a way, we lead to this series.)

2) My collaboration with Christian Frétigny from the prestigious ESPCI permitted, with his idea, to realise a little classification of various sums of a certain given type obtained thanks to the remnants theorem.
For example :

or

You can find this exploration at the page :
Estenave/Fretigny

3) Finally, a little innocent idea of an evening, and hop ! Here comes a series which converge on Pi, simple to put in place, to demonstrate, and looking curiously like BBP's series :

and more generally, if :

so

for p²>1 and with T(n,x) Chebyshev's polynomial.
You can find this algorithm on the page :
Chebyshev