Jacques Bernoulli
(1654 - 1705)

The polynomials of Bernoulli B _N Are defined by recurrence according to :



The numbers (Ber _N ) are then defined by Ber _N =B _N (0)
Other equivalent definition :

The numbers of Bernoulli Ber _K are defined as coefficients in the complete series

=

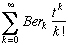
For more information about numerators and denominators of Bernoulli numbers, cf. A027641 and A027642 or about the Ber_2n A000367 and A002445.

Slices of life

First of the lineage of the famous Swiss mathematicians of the same name, Jacques (Jakob) is native of Antwerp but exiles himself under the dictatorship of duke of Albe in Flanders. Abandoning theology important to its father, he turns to mathematics and physics. He will take from the interest for the astronomy his motto " Invito patre sidera verso " (I study stars against the will of my father). Become professor in the university of Basel, he is interested in the infinitesimal calculation that he puts in relation with curves (Lemniscate...) and that allows him to introduce the polar coordinates. He also studies probability and numeric series, that drives him to define the famous numbers of Bernoulli described higher.
* Photos of Johann (1667-1748) and Daniel (1700-1782) Bernoulli

About

Several formulae of analysis appear these numbers of Bernoulli, notably in numerous limits of series as Euler. showed. The contribution in the research on is so fundamental even though it remains indirect. Thanks to him we have the demonstration of the convergence of whose limit and those of the series of this type will be found by Euler.
The first numbers of Bernoulli are :

B₀=1
B₁=-1/2
B₂=1/6
B₄=-1/30
B₆=1/42
B₈=-1/30
B₁₀=5/66